首页课程笔记电子工程系视听信息系统导论

# 循环神经网络 (RNN)

# 网络结构

RNN 的核心在于其能够处理序列数据。在每个时间步 tt，它接收一个输入 x(t)x^{(t)} 和前一个时间步的隐藏层状态 h(t−1)h^{(t-1)}，并计算出当前的隐藏层状态 h(t)h^{(t)} 和输出 y(t)y^{(t)}。

  • 输入: 一个 one-hot 向量 x(t)∈RVx^{(t)} \in \mathbb{R}^V，其中 VV 是词汇表大小。
  • 词向量: e(t)=Ex(t)e^{(t)} = E x^{(t)}。EE 是一个词嵌入矩阵，将 one-hot 向量转换为稠密的词向量。
  • 隐藏层: h(t)=σ(Whh(t−1)+Wee(t)+bh)h^{(t)} = \sigma(W_h h^{(t-1)} + W_e e^{(t)} + b_h)。
    • 这里的 σ\sigma 是激活函数，通常使用 tanh⁡\tanh。
    • WhW_h 是隐藏层到隐藏层的权重矩阵。
    • WeW_e 是输入到隐藏层的权重矩阵。
    • bhb_h 是隐藏层的偏置向量。
  • 输出层: y(t)=softmax(Wyh(t)+by)∈RVy^{(t)} = \text{softmax}(W_y h^{(t)} + b_y) \in \mathbb{R}^V。
    • WyW_y 是隐藏层到输出层的权重矩阵。
    • byb_y 是输出层的偏置向量。

# 优点与缺点

  • 优点:
    1. 可以处理任意长度的输入序列。
    2. 理论上可以利用许多步之前的信息。
    3. 模型大小不会随输入序列的长度增加而变大。
  • 缺点:
    1. 由于循环计算的特性，训练速度较慢。
    2. 容易出现梯度消失和梯度爆炸问题，难以捕捉长距离依赖关系。

# RNN 的训练

训练 RNN 语言模型的目标是最小化预测序列和真实序列之间的交叉熵损失。

  • 单个时间步的损失函数:

    • 在时间步 tt 时，损失函数是预测概率分布 y^(t)\hat{y}^{(t)} 和真实标签 y(t)y^{(t)} 之间的交叉熵。

    J(t)(θ)=CE(y(t),y^(t))=−∑i=1Vyi(t)log⁡y^i(t)=−log⁡y^xt+1(t)J^{(t)}(\theta) = CE(y^{(t)}, \hat{y}^{(t)}) = -\sum_{i=1}^{V} y_i^{(t)} \log \hat{y}_i^{(t)} = -\log \hat{y}_{x_{t+1}}^{(t)}

  • 整个训练集的总损失:

    • 对所有时间步的损失进行平均，得到总损失 J(θ)J(\theta)。

    J(θ)=1T∑t=1TJ(t)(θ)=−1T∑t=1Tlog⁡y^xt+1(t)J(\theta) = \frac{1}{T} \sum_{t=1}^{T} J^{(t)}(\theta) = -\frac{1}{T} \sum_{t=1}^{T} \log \hat{y}_{x_{t+1}}^{(t)}

  • 训练过程:

    • 计算一批次句子的总损失 J(θ)J(\theta)。
    • 使用反向传播算法（通常是时间反向传播，BPTT）计算梯度并更新权重。

# 梯度反向传播

RNN 的训练依赖于反向传播算法，但由于其循环结构，需要一种特殊的形式，即时间反向传播（Backpropagation Through Time, BPTT）。

  • Softmax 与交叉熵损失的梯度:
    • 对于 Softmax 和交叉熵损失的组合，输出层对输入（z=Wyh+byz = W_y h + b_y）的梯度可以简化为：

    ∂L∂z=y^−y\frac{\partial L}{\partial z} = \hat{y} - y

  • 输出层参数的梯度:
    • 对 WyW_y 的梯度：∂L∂Wy=hT(y^−y)\frac{\partial L}{\partial W_y} = h^T (\hat{y} - y)
    • 对 hh 的梯度：∂L∂h=WyT(y^−y)\frac{\partial L}{\partial h} = W_y^T (\hat{y} - y)
    • 对 byb_y 的梯度：∂L∂by=y^−y\frac{\partial L}{\partial b_y} = \hat{y} - y
  • hth_{t} 对 ht−1h_{t-1} 的梯度:
    • 使用 tanh⁡\tanh 激活函数，其导数为 ∂tanh⁡(x)∂x=1−tanh⁡2(x)\frac{\partial \tanh(x)}{\partial x} = 1 - \tanh^2(x)。
    • 链式法则求得 LtL_t 对 ht−1h_{t-1} 的梯度：

    ∂Lt∂ht−1=∂ht∂ht−1∂Lt∂ht=WhTdiag(1−ht2)∂Lt∂ht\frac{\partial L_t}{\partial h_{t-1}} = \frac{\partial h_t}{\partial h_{t-1}} \frac{\partial L_t}{\partial h_t} = W_h^T \text{diag}(1 - h_t^2) \frac{\partial L_t}{\partial h_t}

  • 梯度消失与爆炸问题:
    • 随着时间步的增加，梯度需要通过重复的矩阵乘法向后传播。
    • LtL_t 对 ht−kh_{t-k} 的梯度：

    ∂Lt∂ht−k=∏i=t−k+1t[WhTdiag(1−hi2)]∂Lt∂ht\frac{\partial L_t}{\partial h_{t-k}} = \prod_{i=t-k+1}^{t} \left[ W_h^T \text{diag}(1 - h_i^2) \right] \frac{\partial L_t}{\partial h_t}

    • 如果 ∣∣Wh∣∣||W_h|| 或 ∣∣1−hi2∣∣||1-h_i^2|| 的乘积过小，梯度会趋近于 0（梯度消失）；如果过大，梯度会趋近于无穷（梯度爆炸）。这使得 RNN 很难学习到长距离依赖关系。
  • 对 WhW_h 的梯度:
    • WhW_h 在每个时间步都被使用，因此总梯度是所有时间步梯度的总和。

    ∂Lt∂Wh=∑i=1t∂Lt∂Wh∣i\frac{\partial L_t}{\partial W_h} = \sum_{i=1}^{t} \frac{\partial L_t}{\partial W_h}|_{i}

# RNN 的变种

# 双向 RNN (Bi-RNN)

  • 概念: 同时考虑过去和未来的信息。
  • 结构: 由两个独立的 RNN 组成，一个从前往后处理序列，另一个从后往前处理。最终的输出是两个 RNN 隐藏状态的拼接。
  • 优势: 能够利用完整的上下文信息，在许多自然语言处理任务中表现更好。

# 多层 RNN (Stacked RNN)

  • 概念: 堆叠多个 RNN 层，形成一个更深的网络。
  • 结构: 每一层的输出作为下一层的输入。
  • 应用: 通常，编码器 RNN 使用 2 到 4 层效果最佳，而解码器 RNN 则推荐使用 4 层。更深的 RNN（例如 8 层）需要诸如跳跃连接（skip-connections）等技术来帮助训练。

# 长短期记忆网络 (LSTM)

# 概述

LSTM 是一种特殊的 RNN，其设计旨在解决标准 RNN 的梯度消失问题，能够有效地捕捉长距离依赖。它通过引入门控机制来控制信息的流动。

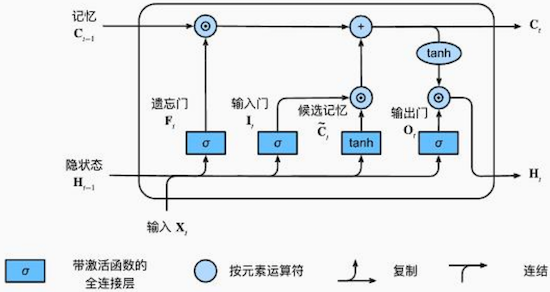
# 核心组件

  • 隐状态 (HtH_t): 类似于 RNN 的隐藏状态，用于传递信息。
  • 记忆（单元状态）(CtC_t): 一条“高速公路”，信息可以在其中畅通无阻地流动，只进行少量的线性操作，从而避免梯度消失。

# 门控机制与更新

LSTM 主要通过以下四个门来控制信息：遗忘门、输入门、候选记忆和输出门。

  1. 遗忘门 (F(t)F^{(t)}): 决定从上一时间步的记忆中丢弃多少信息。

    • 公式: F(t)=σ(WfH(t−1)+UfX(t)+bf)F^{(t)} = \sigma(W_f H^{(t-1)} + U_f X^{(t)} + b_f)

  2. 输入门 (I(t)I^{(t)}): 决定将当前输入中多少新信息加入到记忆中。

    • 公式: I(t)=σ(WiH(t−1)+UiX(t)+bi)I^{(t)} = \sigma(W_i H^{(t-1)} + U_i X^{(t)} + b_i)

  3. 候选记忆 (C~(t)\tilde{C}^{(t)}): 这是一个新的候选记忆向量，由当前输入和上一时间步的隐状态生成。

    • 公式: C~(t)=tanh⁡(WcH(t−1)+UcX(t)+bc)\tilde{C}^{(t)} = \tanh(W_c H^{(t-1)} + U_c X^{(t)} + b_c)

  4. 单元状态更新 (C(t)C^{(t)}): 结合遗忘门和输入门来更新记忆。

    • 公式: C(t)=F(t)⊙C(t−1)+I(t)⊙C~(t)C^{(t)} = F^{(t)} \odot C^{(t-1)} + I^{(t)} \odot \tilde{C}^{(t)}
    • F(t)⊙C(t−1)F^{(t)} \odot C^{(t-1)}: 保留上一时间步的部分记忆。
    • I(t)⊙C~(t)I^{(t)} \odot \tilde{C}^{(t)}: 添加当前时间步的新信息。

  5. 输出门 (O(t)O^{(t)}): 决定将更新后的记忆中多少信息暴露给隐状态。

    • 公式: O(t)=σ(WoH(t−1)+UoX(t)+bo)O^{(t)} = \sigma(W_o H^{(t-1)} + U_o X^{(t)} + b_o)

  6. 隐状态更新 (H(t)H^{(t)}): 将更新后的记忆通过 tanh⁡\tanh 激活函数，并与输出门相乘，得到最终的隐状态。

    • 公式: H(t)=O(t)⊙tanh⁡(C(t))H^{(t)} = O^{(t)} \odot \tanh(C^{(t)})

# 优点与缺点

  • 优势:
    • 有效处理长距离依赖: 在实际应用中，LSTM 可以在大约 100 个时间步的跨度内保留信息，远优于标准 RNN（通常只能维持约 7 个时间步）。
  • 缺点:
    • 线性交互距离: LSTM 仍需 O(sequence length)O(\text{sequence length}) 步才能使相隔很远的词对产生相互作用。这使得它很难捕捉到非线性的远距离依赖关系，且线性顺序并非总能正确地反映句子的语义结构。
    • 串行计算: 其循环特性决定了它只能进行串行计算，无法进行并行化处理，导致训练效率较低。