# 视觉信息处理# 线性平移不变的图像滤波线性平移不变滤波器通常被定义为卷积操作,通过对图像和卷积核进行加权求和来实现。
( g ∗ f ) ( x , y ) = ∫ − ∞ ∞ g ( y ) f ( x − y ) d y ( g ∗ f ) ( x , y ) = ∑ i = − ∞ ∞ g ( i , j ) I ( x − i , y − j ) (g*f)(x, y) = \int_{-\infty}^{\infty} g(y) f(x - y) dy
(g*f)(x, y) = \sum_{i=-\infty}^{\infty} g(i, j) I(x - i, y - j)
( g ∗ f ) ( x , y ) = ∫ − ∞ ∞ g ( y ) f ( x − y ) d y ( g ∗ f ) ( x , y ) = i = − ∞ ∑ ∞ g ( i , j ) I ( x − i , y − j )
1. 可拆分的滤波器
一个二维可拆分的滤波器可以写作一个列向量滤波器和一个行向量滤波器的乘积。对于一个 M × M M \times M M × M N × N N \times N N × N O ( M 2 N 2 ) O(M^2N^2) O ( M 2 N 2 ) O ( 2 N M 2 ) O(2NM^2) O ( 2 N M 2 )
2. 常用滤波器
3. 边缘检测
由于微分操作对噪声非常敏感,边缘检测通常需要先进行平滑处理。
DoG(高斯滤波器的导数) :一阶滤波器。通过卷积/导数换序定理进行计算,图像边缘的亮度在滤波后会呈现峰值。LoG(高斯-拉普拉斯) :高斯滤波器的二阶导。边缘两侧的亮度呈现峰值,因此零交叉(Zero-crossing)点可以更精确地定位边缘,但实现起来不如 DoG 方便。二维 DoG :根据梯度方向,可进行带方向的边缘检测。二维 LoG :不带方向,表达式为 Δ h σ ( u , v ) \Delta h_{\sigma}(u, v) Δ h σ ( u , v ) 在离散图像处理中,微分通常用有限差分 来近似。
4. 有限差分
有限差分公式:f ′ ( x ) = ( f ( x + 1 ) − f ( x − 1 ) ) / 2 f'(x) = (f(x + 1) - f(x - 1))/2 f ′ ( x ) = ( f ( x + 1 ) − f ( x − 1 )) /2
Sobel 滤波器 :DoG 的常见近似。
水平 Sobel 滤波器 :对水平方向的变化敏感,用于检测垂直方向的轮廓。s x = 1 8 [ 1 0 − 1 2 0 − 2 1 0 − 1 ] = 1 8 [ 1 2 1 ] [ 1 0 − 1 ] s_x = \frac18 \begin{bmatrix} 1 & 0 & -1 \\ 2 & 0 & -2 \\ 1 & 0 & -1 \end{bmatrix} = \frac18 \begin{bmatrix} 1 \\ 2 \\ 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & -1 \end{bmatrix}
s x = 8 1 1 2 1 0 0 0 − 1 − 2 − 1 = 8 1 1 2 1 [ 1 0 − 1 ]
垂直 Sobel 滤波器 :对垂直方向的变化敏感,用于检测水平方向的轮廓。s y = 1 8 [ 1 2 1 0 0 0 − 1 − 2 − 1 ] = 1 8 [ 1 0 − 1 ] [ 1 2 1 ] s_y = \frac18 \begin{bmatrix} 1 & 2 & 1 \\ 0 & 0 & 0 \\ -1 & -2 & -1 \end{bmatrix} = \frac18 \begin{bmatrix} 1 \\ 0 \\ -1 \end{bmatrix} \begin{bmatrix} 1 & 2 & 1 \end{bmatrix}
s y = 8 1 1 0 − 1 2 0 − 2 1 0 − 1 = 8 1 1 0 − 1 [ 1 2 1 ]
梯度计算 :
通过水平和垂直 Sobel 滤波器对图像进行卷积,可以得到水平和垂直梯度 f x f_x f x f y f_y f y
梯度振幅:∣ ∣ ∇ f ∣ ∣ = f x 2 + f y 2 ||\nabla f|| = \sqrt{f_x^2 + f_y^2} ∣∣∇ f ∣∣ = f x 2 + f y 2
梯度方向:θ = arctan ( f y / f x ) \theta = \arctan(f_y/f_x) θ = arctan ( f y / f x )
# 用于模板匹配的滤波器模板匹配通过滤波器核来计算图像与模板的相似度。
相关运算(Correlation) :最简单的模板匹配方法,但受亮度绝对值影响。h [ m , n ] = ∑ k , l g [ k , l ] f [ m + k , n + l ] h[m, n] = \sum_{k, l} g[k, l] f[m+k, n+l]
h [ m , n ] = k , l ∑ g [ k , l ] f [ m + k , n + l ]
使用零均值模板 :速度最快,但对局部强度非常敏感。h [ m , n ] = ∑ k , l ( g [ k , l ] − g ˉ ) f [ m + k , n + l ] h[m, n] = \sum_{k, l} (g[k, l] - \bar g) f[m+k, n+l]
h [ m , n ] = k , l ∑ ( g [ k , l ] − g ˉ ) f [ m + k , n + l ]
差异的平方和(SSD) :中等速度,结合阈值可用于基本检测,但对强度偏移敏感。h [ m , n ] = ∑ k , l ( g [ k , l ] − f [ m + k , n + l ] ) 2 h[m, n] = \sum_{k, l} (g[k, l] - f[m+k, n+l])^2
h [ m , n ] = k , l ∑ ( g [ k , l ] − f [ m + k , n + l ] ) 2
归一化互相关(NNC) :速度最慢,但对对比度和亮度变化具有不变性。h [ m , n ] = ∑ k , l ( g [ k , l ] − g ˉ ) ( f [ m + k , n + l ] − f ˉ m , n ) ∑ k , l ( g [ k , l ] − g ˉ ) 2 ∑ k , l ( f [ m + k , n + l ] − f ˉ m , n ) 2 h[m, n] = \frac{\sum_{k, l} (g[k, l] - \bar g) (f[m+k, n+l] - \bar f_{m, n})}{\sqrt{\sum_{k, l} (g[k, l] - \bar g)^2 \sum_{k, l} (f[m+k, n+l] - \bar f_{m, n})^2}}
h [ m , n ] = ∑ k , l ( g [ k , l ] − g ˉ ) 2 ∑ k , l ( f [ m + k , n + l ] − f ˉ m , n ) 2 ∑ k , l ( g [ k , l ] − g ˉ ) ( f [ m + k , n + l ] − f ˉ m , n )
# 图像采样与金字塔1. 朴素下采样
通过直接删除像素来降低图像分辨率,但容易出现混叠(Aliasing)。
混叠 :在下采样过程中,一个高频信号可能被错误地表示为较低频率的信号。图像中的混叠 :通常表现为摩尔纹。
2. 抗混叠
上采样 :提高分辨率,但需要达到奈奎斯特定理的采样频率才能避免混叠。平滑处理 :在下采样前,先通过平滑滤波器去除可能导致混叠的高频信息。虽然会丢失部分信息,但效果优于混叠。
奈奎斯特定理 :如果对一个模拟信号以大于其最高频率两倍的速率进行均匀采样,则可以从离散的采样值中完全恢复原始信号。
3. 图像金字塔
高斯金字塔 :
从底层到顶层,图像尺寸和像素数量逐渐减少。
通过重复滤波和平滑 操作,然后进行下采样 来构建,这是一个有损过程。
拉普拉斯金字塔 :
从顶层到底层,图像尺寸逐渐增加。
通过重复上采样 和残差相加 来恢复图像。
该过程保留了残差 ,因此是无损的。
# 视觉信息编码# 图像压缩编码技术1. 图像压缩的目的
在有限存储空间中存储更多数据。
降低数据传输和运输成本,最小化带宽消耗。
加快图像处理和传输速度。
2. 冗余类别
时间冗余 :相邻帧之间的相似性。空间冗余 :相邻像素之间的强相关性。编码冗余 :不同像素值出现的概率不同。视觉冗余 :人眼对某些细节不敏感。知识冗余 :可从先验知识中获得的信息。
3. 压缩类型
无损压缩 :压缩比较低(约 1/2 到 1/3),如 Wiinzip, JPEG-LS。有损压缩 :压缩比较高(约 1/10 到 1/20),如 MPEG-2。
4. 通信系统组成
信号源 → 编码器 → 通道 → 解码器 → 信号目的地。
5. 图像源编码分类
利用冗余 来减少信息熵,实现无损编码 。
利用视觉冗余 ,在不影响视觉感知的前提下实现有损压缩 。
6. 消除时空相关性的方法
预测编码 :利用相邻像素之间的相关性,根据已编码的像素值预测当前像素的值。
差分编码(Differential Coding) 可变长度编码(Run-Length Encoding, RLE)
# 视频图像的帧间预测利用视频序列中相邻帧的相似性进行压缩。
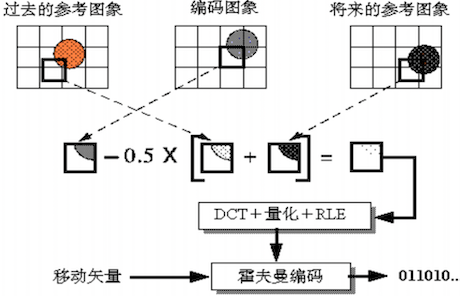
I 帧(关键帧) :帧内编码,不依赖其他帧,可独立解码。P 帧(预测帧) :前向预测,通过运动估计 和运动补偿 技术,预测当前帧与前一个 I 或 P 帧之间的差异。B 帧(双向预测帧) :使用过去的一个 I/P 帧和未来的一个 I/P 帧进行编码,进一步提高效率,但增加了复杂性。
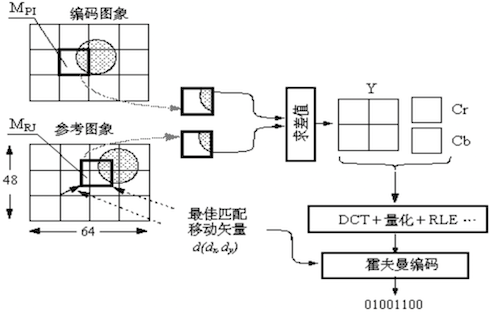
运动补偿 :将帧分割成宏块(macroblocks),分析每个宏块的运动,确定其在预测帧中的最佳匹配位置。
图像块匹配 :利用 MSE(最小均方差)或 MAD(最小平均绝对差)来确定参考帧中的宏块在预测帧中的最佳匹配。编码 :对预测帧与实际帧之间的差异进行编码,进一步减少数据量。
P 帧预测编码图例:
B 帧预测编码图例:
# 变换编码通过数学变换(如 DCT、小波变换)将图像数据转换到频域,再对变换系数进行量化和编码。由于图像能量多集中在低频成分,可以舍弃高频成分以实现高压缩比。
目的 :
移除空间相关性。
将空间信号的能量集中在少量低频系数上。
通过量化去除小系数,同时不显著影响重建图像质量。
离散余弦变换(DCT) :
F ( u , v ) = 1 4 C ( u ) C ( v ) ∑ x = 0 N − 1 ∑ y = 0 N − 1 f ( x , y ) cos ( ( 2 x + 1 ) u π 2 N ) cos ( ( 2 y + 1 ) v π 2 N ) f ( x , y ) = 1 4 ∑ u = 0 N − 1 ∑ v = 0 N − 1 C ( u ) C ( v ) F ( u , v ) cos ( ( 2 x + 1 ) u π 2 N ) cos ( ( 2 y + 1 ) v π 2 N ) C ( u ) , C ( v ) = { 1 2 , u = 0 or v = 0 1 , otherwise N = 8 F(u, v) = \frac14 C(u) C(v) \sum_{x=0}^{N-1} \sum_{y=0}^{N-1} f(x, y) \cos(\frac{(2x + 1)u\pi}{2N}) \cos(\frac{(2y + 1)v\pi}{2N}) \\
f(x, y) = \frac14 \sum_{u=0}^{N-1} \sum_{v=0}^{N-1} C(u) C(v) F(u, v) \cos(\frac{(2x + 1)u\pi}{2N}) \cos(\frac{(2y + 1)v\pi}{2N}) \\
C(u), C(v) = \begin{cases} \frac{1}{\sqrt{2}}, & u = 0 \text{ or } v = 0 \\ 1, & \text{otherwise} \end{cases} \\
N = 8
F ( u , v ) = 4 1 C ( u ) C ( v ) x = 0 ∑ N − 1 y = 0 ∑ N − 1 f ( x , y ) cos ( 2 N ( 2 x + 1 ) u π ) cos ( 2 N ( 2 y + 1 ) v π ) f ( x , y ) = 4 1 u = 0 ∑ N − 1 v = 0 ∑ N − 1 C ( u ) C ( v ) F ( u , v ) cos ( 2 N ( 2 x + 1 ) u π ) cos ( 2 N ( 2 y + 1 ) v π ) C ( u ) , C ( v ) = { 2 1 , 1 , u = 0 or v = 0 otherwise N = 8
量化技术 :
将绝对值小于特定阈值(如 40)的 DCT 系数置为零。
对所有系数进行四舍五入到整数。
使用预定义的量化矩阵。
# 统计编码根据符号出现的概率对符号进行编码,如霍夫曼编码,使平均码长接近信息熵。
源信息熵 :H = − ∑ i = 1 n p i log 2 p i H = -\sum_{i=1}^{n} p_i \log_2 p_i H = − ∑ i = 1 n p i log 2 p i 平均代码长度 :L ˉ = ∑ i = 1 n p i l i \bar L = \sum_{i=1}^{n} p_i l_i L ˉ = ∑ i = 1 n p i l i 编码效率 :η = H / L ˉ \eta = H / \bar L η = H / L ˉ 压缩比 :k = 自然二进制码长 / L ˉ k = \text{自然二进制码长} / \bar L k = 自然二进制码长 / L ˉ 码方差 :σ 2 = E ( l i − L ˉ ) 2 \sigma^2 = E (l_i - \bar L)^2 σ 2 = E ( l i − L ˉ ) 2 冗余度 :r = 1 − η r = 1 - \eta r = 1 − η 霍夫曼编码约定 :左子路为 0,右子路为 1,将概率较小的数放在右子路。