1. 特征工程

# 降维：主成分分析（PCA）

# 算法概述

PCA 是一种无监督的降维算法，其核心思想是在保留数据最大方差的前提下，将高维数据映射到低维空间。

# 算法步骤

1. 数据准备：假设每个样本有 $k$ 个特征，共 $n$ 个样本。每个样本 $x$ 是一个 $k \times 1$ 的列向量。
2. 中心化：计算所有样本的均值 $\overline{x}$，将每个样本减去均值以进行中心化处理，即 $x_{centered} = x - \overline{x}$。中心化的目的是防止主成分方向偏向于数据中均值过大的特征。
3. 归一化（可选）：若不同特征的单位不统一，可以计算每个特征的方差并进行归一化。这确保了每个特征对主成分的贡献是平等的，防止主成分方向偏向于方差更大的方向。
4. 构建矩阵：将所有中心化后的样本合并，形成一个 $k \times n$ 的矩阵 $X$。
5. 计算协方差矩阵：计算协方差矩阵 $M = XX^T$，其维度为 $k \times k$。
6. 特征值分解：对 $M$ 进行特征值分解，得到 $k$ 个特征值 $\lambda_1, \lambda_2, \ldots, \lambda_k$ 和对应的特征向量（主成分）$e_1, e_2, \ldots, e_k$。
7. 投影：任取一个样本 $x^{(i)}$，其在特征空间中可表示为 $x^{(i)} = \overline{x} + \sum_j g_{j}^{(i)} e_j$，其中第 $j$ 个主成分的坐标为 $g_{j}^{(i)} = e_j^T(x^{(i)}-\overline{x})$。
8. 降维：为了实现降维，通常只保留那些特征值较大的前 $m$ 个主成分，即对应的前 $m$ 个特征向量。

# 算法性质与细节

• 方差与协方差：某个维度的主成分方差等于其对应的特征值，即 $var(g_k) = \lambda_k$。不同维度主成分之间的协方差为零，即 $cov(g_k, g_j) = 0$。
• 总方差：主成分方差之和等于原始特征方差之和，即 $\sum_k var(g_k) = \sum_k var(x_k) = \sum_k \lambda_k$。
• 相关系数：原始特征 $x_j$ 与主成分 $g_i$ 的相关系数为 $\rho_{g_i, x_j} = \frac{e_{ij}\sqrt{\lambda_i}}{\sqrt{\sigma_{jj}}}$，表示 $x_j$ 能被 $g_i$ 解释的部分。所有主成分对任意一个原始特征的解释程度平方和为 1，即 $\sum_i \rho_{g_i, x_j}^2 = 1$。
• 坐标系：新坐标系的轴线沿着主成分（特征向量）方向。若样本经过中心化，新坐标系的原点位于样本均值处；否则，原点仍在 $(0,0)$。
• 计算复杂度：
  • 计算所有特征值和特征向量的复杂度为 $O(k^3)$。
  • 计算前 $m$ 个特征值和特征向量的复杂度为 $O(mk^2)$。
  • 优化方法：可使用随机化 PCA（快速寻找近似解）和增量 PCA（降低内存开销）来降低复杂度，或利用奇异值分解（SVD）近似。

---

# 图像特征：角点检测与常用滤波器

# Harris 角点检测

Harris 角点检测是一种用于识别图像中角点的经典算法。

# 算法步骤

1. 区域划分与梯度计算：将图像划分为多个小区域，计算每个小区域内每个像素的 $x$ 和 $y$ 方向的梯度 $I_x, I_y$。梯度可通过差分或 Sobel 等卷积核来计算。
2. 构建协方差矩阵：对每个小区域，构建一个 $2 \times 2$ 的协方差矩阵 $M$：

   $$M = \begin{bmatrix} \sum I_x^2 & \sum I_xI_y \\ \sum I_yI_x & \sum I_y^2 \end{bmatrix}$$

3. 特征值分析：计算矩阵 $M$ 的特征值 $\lambda_1$ 和 $\lambda_2$。
   • 平滑点：$\lambda_1, \lambda_2 \approx 0$。
   • 边界：$\lambda_1 \gg \lambda_2$（垂直方向）或 $\lambda_1 \ll \lambda_2$（水平方向）。
   • 角点：$\lambda_1, \lambda_2$ 均较大且差异不明显。
4. 角点响应值：通过角点响应值 $R$ 定量判断，其中 $R = \det(M) - k \cdot \text{tr}^2(M) = \lambda_1\lambda_2 - k(\lambda_1+\lambda_2)^2$。
   • $R \approx 0$：平滑点。
   • $R < 0$：边界。
   • $R > 0$：角点。
5. 非极大值抑制：对所有角点响应值进行非极大值抑制，以筛选出真正的角点。

# 算法特点

• 旋转不变性：算法对图像旋转不敏感。
• 尺度敏感性：算法对图像尺度变化敏感。

# 常用滤波器

# Gaussian 滤波器

• 作用：用于图像平滑和去噪。
• 表达式：

  $$G(x, y) = \frac{1}{2\pi\sigma^2} \exp \left( -\frac{x^2 + y^2}{2\sigma^2} \right)$$

• 卷积核：一个 $3 \times 3$ 的常见卷积核为 $\frac{1}{16} \begin{bmatrix} 1&2&1\\ 2&4&2\\ 1&2&1 \end{bmatrix}$。卷积核的权重归一化是为了防止图像亮度发生变化。

# Sobel 滤波器

• 作用：用于边缘检测，基于一阶导数。
• 算子：$\nabla f(x, y) = \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}$。
• 卷积核：常用的 $3 \times 3$ 卷积核有：

  $$S_x = \begin{bmatrix} -1&0&1\\ -2&0&2\\ -1&0&1 \end{bmatrix},\quad S_y = \begin{bmatrix} -1&-2&-1\\ 0&0&0\\ 1&2&1 \end{bmatrix}$$

# Laplacian 滤波器

• 作用：用于边缘检测或尺度检测，基于二阶导数。
• 算子：$\Delta f(x, y) = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}$。
• 卷积核：常用的 $3 \times 3$ 卷积核有：

  $$\begin{bmatrix} 0&1&0\\ 1&-4&1\\ 0&1&0 \end{bmatrix} \text{或} \begin{bmatrix} -1&-1&-1\\ -1&8&-1\\ -1&-1&-1 \end{bmatrix}$$

# LoG (Laplace of Gaussian) 滤波器

• 作用：边缘检测，将拉普拉斯算子应用于高斯函数。
• 表达式：

  $$\text{LoG}(x, y) = \frac{1}{\pi \sigma^4} \left( 1 - \frac{x^2 + y^2}{2\sigma^2} \right) \exp \left( -\frac{x^2 + y^2}{2\sigma^2} \right)$$

# DoG (Difference of Gaussian) 滤波器

• 作用：边缘检测，通过对图像应用不同标准差的高斯滤波器后进行差分得到。
• 特点：可以很好地近似 LoG 滤波器。

---

# 图像匹配

# 常用匹配方法

# 模板匹配

• 特点：对各种变换（旋转、尺度、亮度等）都非常敏感。

# 梯度匹配

• 特点：对图像强度的绝对值变化不敏感。

# 颜色直方图 (Color Histogram)

• 原理：计算图像中不同颜色的像素数量并绘制直方图。
• 特点：对旋转和尺度变化不敏感，但没有考虑空间位置信息。

# 空间直方图 (Spatial Histogram)

• 原理：将图像分割成多个小区域（cell），并对每个 cell 分别计算颜色直方图。
• 特点：弥补了颜色直方图的不足，对部分空间变换不敏感。

# 基于特征的匹配方法

# SIFT (Scale Invariant Feature Transform)

• 特点：对旋转、尺度和亮度变化具有不变性。
• 核心思想：
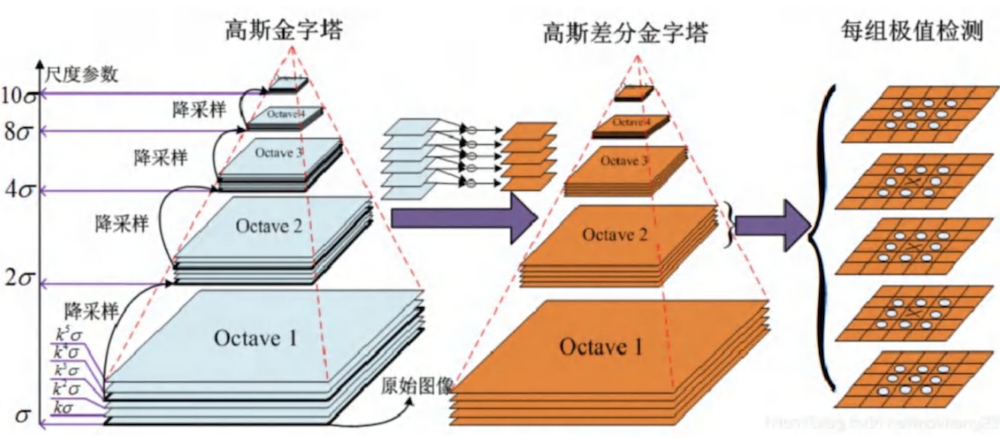
  1. 尺度空间构建：通过不同尺度的 Gaussian 滤波器构建图像金字塔（八度）。在同一八度内，对图像应用不同尺度的 Gaussian 卷积核；在相邻八度之间，通过降采样获得图像。
  2. 关键点检测：对相邻尺度的 Gaussian 图像进行差分得到 DoG 图像，然后对每个像素进行非极大值抑制，比较其在尺度空间（同一层 8 个，上下层各 9 个）共 26 个邻域点的值，找到局部极值点作为潜在关键点。
  3. 关键点精确定位：使用二次泰勒展开对 DoG 函数进行拟合，精确定位关键点的位置。
  4. 方向赋值：根据关键点邻域像素的梯度方向直方图，确定关键点的主方向，从而实现旋转不变性。

# SURF (Speeded Up Robust Features)

• 特点：比 SIFT 速度更快，对模糊和旋转具有鲁棒性，但对视角和光照变化敏感。
• 核心思想：
  1. Box Filter 近似：使用 Box Filter 来近似 DoG 滤波器。
  2. 积分图：利用积分图（Integral Image）技术快速计算 Box Filter 的卷积值，大幅提高计算速度。

# 学习型方法 (Learning based)

• 特点：
  • 鲁棒性：对比例、遮挡、形变和旋转等变换更具鲁棒性。
  • 性能：在特定任务上能超越传统方法。
  • 缺点：训练耗时，需要大量数据集；泛化性可能较差，难以在不同场景中可靠泛化。

---

# 监督学习：线性回归与 SVM

# 线性回归

# 目标与损失函数

• 目标：找到一组参数 $\theta \in \R^d$，使得模型 $h_\theta(x^{(i)}) = \theta^T x^{(i)}$ 能够拟合目标值 $y^{(i)}$。
• 目标函数：采用最小二乘法 (LSE)，旨在最小化预测值与真实值之间的平方误差和：

  $$\min_\theta L(\theta) = \frac12 \sum_{i}\left( h_\theta(x^{(i)}) - y^{(i)} \right)^2$$

# 求解方法

1. 闭式解：
   • 将目标函数写成矩阵形式 $L(\theta) = \frac12 (X\theta - Y)^T(X\theta - Y)$。
   • 通过对 $\theta$ 求梯度并令其为零，得到闭式解：$\hat \theta = (X^TX)^{-1}X^TY$。
2. 梯度下降 (GD) 法：
   • 迭代更新：$\theta^{t+1} = \theta^t - \alpha \nabla_\theta L(\theta)$，其中 $\alpha$ 是学习率。
   • 学习率：学习率可以采用线性或指数衰减策略。
   • 随机梯度下降 (SGD)：每次迭代仅使用一个小批量（mini-batch）的数据来计算梯度。
   • SGD 的优缺点：
     • 优点：加快损失计算速度、降低内存消耗、具备更好的局部最优跳跃能力。
     • 缺点：收敛速度变慢、震荡性强、不稳定。
   • 避免局部最优：可使用动量法等高级优化器、在梯度中增加随机噪声或使用分批次的训练数据。

# 矩阵求导法则

• 基本规则：$\nabla_x f(x)$ 的第 $ij$ 个元素为 $\frac{\partial f_j}{\partial x_i}$。
• 常用公式：
  • $\nabla_x Ax = A^T$
  • $\nabla_x x^TA = A$
  • $\nabla_x x^TAx = (A+A^T)x$
  • $\nabla_A \text{tr}(AB) = B^T$

# 支持向量机 (SVM)

# 目标与求解

• 目标：找到一个能够最大化两类样本到分界面距离（间隔）的分界面 $w^Tx+b=0$。
• 目标函数：通过约束优化，将问题转化为：

  $$\min_{w, b} \frac12 \|w\|_2^2 \quad s.t. \quad y^{(i)}(w^Tx^{(i)}+b) \ge 1$$

• 对偶问题：通过引入拉格朗日乘子，该问题可转化为对偶问题：

  $$\max_\alpha \quad L(\alpha) = \sum_i \alpha_i - \frac12 \sum_{i, j} y^{(i)}y^{(j)}\alpha_i\alpha_j x^{(i)T}x^{(j)} \\ s.t. \quad \sum_i \alpha_i y^{(i)}=0, \quad \alpha_i \ge 0$$

# 优化与预测

• 优化方法：
  • 二次规划 (QP)：SVM 的对偶问题是一个二次规划问题。
  • SMO 算法：通过每次只选择两个变量进行迭代优化，将复杂问题分解为简单的子问题。
• 预测：得到最优解 $\alpha^*$ 后，可以计算 $w^* = \sum_{i \in SV} \alpha_i y^{(i)}x^{(i)}$ 和 $b^*$，然后使用 $\hat y_{test} = \text{sign}(w^{*T}x_{test}+b^*)$ 进行预测。

# 非线性 SVM

• 核函数：通过将内积 $x^{(i)T}x^{(j)}$ 替换为核函数 $K(x^{(i)}, x^{(j)}) = \phi(x^{(i)})^T\phi(x^{(j)})$，将数据从原始空间映射到更高维的特征空间，从而解决非线性问题。
• 常用核函数：多项式核、高斯（RBF）核和 Sigmoid 核。

---

# 深度学习基础

# 常用分类器

# 逻辑回归

• 激活函数：使用 Sigmoid 函数 $\sigma(z) = \frac{1}{1 + \exp(-z)}$ 将线性输出映射到 $(0,1)$ 区间。
• 损失函数：通常使用交叉熵损失：

  $$L(y, \hat y) = -y \log(\hat y) - (1-y) \log(1-\hat y)$$

# 多分类

• Softmax 函数：将多个线性输出转换为概率分布，$\hat y_i = \frac{\exp(z_i)}{\sum_j \exp(z_j)}$。
• 交叉熵损失：用于多分类任务，当 $y$ 为 one-hot 向量时，损失为 $L = -\sum_j y_j \log(\hat y_j)$。

# 聚类

• K-Means 算法：
  • 分类：将每个样本分配到与其距离最近的中心点。
  • 更新：将每个簇的中心点更新为该簇中所有样本的均值。

# 神经网络

# 激活函数

• Sigmoid：$1/(1+e^{-x})$。
• tanh：$\tanh(x)$。
• ReLU：$\max(0, x)$，简单高效，但可能出现神经元死亡问题。
• Leaky ReLU：$\max(0.1x, x)$，解决了 ReLU 的神经元死亡问题。
• ELU：$x$ (for $x>0$)；$\alpha(e^x-1)$ (for $x < 0$)。

# 反向传播 (BP) 算法

• 计算方式：通常从网络输出端向输入端计算梯度，因为损失函数是标量，维度较低。
• 特点：可以有效避免重复计算，提高效率。

# 优化器

• 动量法：通过累积梯度来加速收敛，使用 $\beta v_{t-1} + (1-\beta) \nabla_\theta J(\theta)$ 更新动量。
• RMSProp：自适应学习率，防止学习率过快或过慢。
• Adam：结合了动量法和 RMSProp 的优点，是目前最常用的优化器之一。

# 正则化

• 目的：缓解模型过拟合。
• L1/L2 正则：在损失函数中增加参数的范数惩罚项，L1 倾向于产生稀疏解。
• Dropout：在训练时随机使部分神经元失活，迫使网络学习冗余表示，防止特征的共适应性。

# 批标准化 (Batch Normalization)

• 原理：在网络每一层对 mini-batch 的输入进行归一化。
• 作用：加速训练、允许使用更大的学习率、减少对初始化的敏感性。
• 可学习参数：引入可学习的 $\gamma$ 和 $\beta$ 参数，以恢复模型的表达能力。

# 参数初始化

• 重要性：不能将所有参数初始化为零或相同的值，否则所有神经元将学习相同的特征。
• Xavier 初始化：适用于 Sigmoid 和 tanh 激活函数，其方差为 $\frac{2}{n_{in}+n_{out}}$。

# 超参数调优

• 常见超参数：批次大小、学习率、动量、初始化方法、正则化参数、网络架构等。
• 调优策略：通常采用从粗粒度到细粒度的搜索策略，如网格搜索或随机搜索，并且可以通过在小数据集上观察模型是否过拟合来快速判断超参数的有效性。