10. 一维原子链的振动

# 晶格模型与绝热近似

# 静止晶格模型的局限性

静止晶格模型无法解释固体的许多重要物理性质。在这种模型中，原子被固定在平衡位置，无法振动，这导致：

无法解释热性质： 晶格的振动是固体比热、热膨胀等平衡性质的根本来源，也是热传导等输运性质的重要机制。静止模型无法解释这些现象。
电导率“无限大”： 根据布洛赫定理，电子在严格周期性势场中运动时不会发生散射，因此电导率将是无限大。然而，实际晶体中存在原子振动，这打破了严格的周期性，为电子提供了散射机制，从而使电导率有限。
绝缘体是“绝热体”： 在静止晶格模型下，绝缘体中的电子处于满带，无法参与输运过程，因此模型无法解释绝缘体丰富的物理性质，例如热传导。实际上，晶格振动在绝缘体的热传导中起着主导作用。

# 绝热近似（Born-Oppenheimer Approximation）

绝热近似，也称为定核近似，是解决上述局限性的关键。其核心思想是：分子系统中原子核的运动与电子的运动可以分离。由于电子的运动速度远高于原子核，我们可以将固体系统分为两个子系统：

电子系统： 研究电子运动时，可以近似认为原子核是静止不动的。这构成了固体电子论的基础。
原子核系统： 研究原子核的运动时，可以将其看作整个中性原子的运动，而不需要考虑空间中电子的分布。这构成了晶格振动理论的基础。

# 一维原子链的振动

# 一维单原子链模型

这个模型简化了晶体结构，用于研究晶格振动的基本特性。

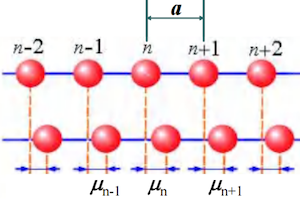
模型假设： 原子被限制在沿链的方向运动，只考虑非平衡状态下的纵向振动。
参数设定： 原子质量为 $m$ ，平衡状态下原子间距为 $a$ 。
位移表示： 非平衡时，第 $n$ 个原子偏离平衡位置的位移用 $\mu_n$ 表示。第 $n$ 个原子和第 $n+1$ 个原子之间的距离变为 $a+(\mu_{n+1}-\mu_n)$ 。

# 晶格振动方程与色散关系

振动方程： 假设只有相邻原子间存在相互作用。利用简谐近似（保留势能泰勒展开的 $\delta^2$ 项），相邻原子间的相互作用力与位移差成正比。第 $n$ 个原子所受的总作用力为 $F_n = \beta(\mu_{n+1}+\mu_{n-1}-2\mu_n)$ ，其中 $\beta$ 是恢复力常数。根据牛顿第二定律，运动方程为：

$m\ddot{\mu}_n=\beta(\mu_{n+1}+\mu_{n-1}-2\mu_n)$

这是一个相邻原子间的耦合运动方程组。
简谐振动解： 联立所有原子的运动方程，可以得到简谐振动形式的解：

$\mu_n=Ae^{i(wt-qX_n)}$

其中 $X_n$ 是第 $n$ 个原子的平衡位置 $na$ 。所有原子以相同的频率 $w$ 和振幅 $A$ 振动，但相邻原子之间存在相位差 $qa$ 。
色散关系： 将简谐解代入运动方程，可以得到频率 $w$ 与波数 $q$ 之间的关系，即色散关系：

$w^2=\frac{2\beta}{m}(1-\cos(aq))=\frac{4\beta}{m}\sin^2(\frac{aq}{2})$

# 格波与第一布里渊区

原子在平衡位置附近的振动以波的形式在晶体中传播，这种波称为格波。格波的波长 $\lambda=2\pi/q$ 。

两种特殊情况的格波：
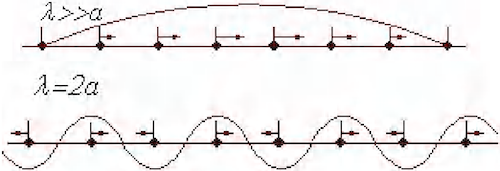
第一布里渊区： 当波数 $q$ 变化 $2\pi/a$ 时，原子位移不变。因此，只需考虑 $q$ 在一个特定范围内的独立值，这个范围就是线晶格的第一布里渊区： $-\pi/a<q\le\pi/a$ 。

# 周期性边界条件（Born-Kármán Condition）

为了处理有限晶体，我们引入周期性边界条件，将晶体抽象为首尾相连的环状链。

条件： 设晶体链中有 $N$ 个原子，链长为 $Na$ 。周期性边界条件为 $\mu_{N+n}=\mu_n$ 。
结果： 周期性边界条件导致 $q$ 的取值是离散的： $q=\frac{2\pi h}{Na}$ ，其中 $h$ 为整数。
$q$ 的分布： $q$ 的分布密度为 $\rho(q)=\frac{Na}{2\pi}=\frac{L}{2\pi}$ 。在第一布里渊区内，波数 $q$ 的取值总数为 $N$ ，即等于晶体链中原胞的数量。

# 格波的频率与速度

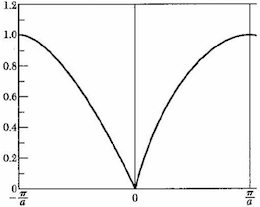
色散关系曲线： 根据色散关系 $w=2\sqrt{\frac{\beta}{m}}\left|\sin(\frac{aq}{2})\right|$ ，我们可以绘制 $w-q$ 曲线。
- 截止频率（最大频率）： $w_m=2\sqrt{\frac{\beta}{m}}$ 。
速度：
- 相速度 $v_p$ ： 单色波传播的速度，定义为 $v_p=w/q$ 。
- 群速度 $v_g$ ： 波包传播的速度，代表能量和动量的传播速度，定义为 $v_g=dw/dq$ 。
特殊情况：
- 第一布里渊区边界（ $q=\pm\pi/a$ ）： 此时群速度 $v_g=0$ ，发生布拉格反射，形成驻波。格波波长 $\lambda=2a$ ，相邻原子振动相位相反。
- 长波极限（ $q\to0$ ）： 此时群速度和相速度相等，为 $a\sqrt{\beta/m}$ 。这类似于连续介质的弹性波，在长波极限下可将晶格视为连续介质。

# 一维双原子链的振动

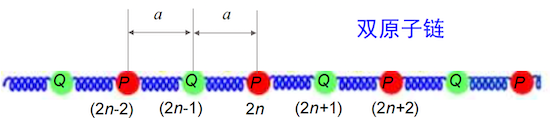
# 一维双原子链结构

考虑最简单的双原子链模型，即原胞中包含两个质量不同的原子，P 原子质量为 $m$ ，Q 原子质量为 $M>m$ 。

# 运动方程与色散关系

运动方程： 类似单原子链，我们可以写出 P 原子和 Q 原子的运动方程：

$m\ddot{\mu}_{2n}=\beta(\mu_{2n+1}+\mu_{2n-1}-2\mu_{2n}) \\ M\ddot{\mu}_{2n+1}=\beta(\mu_{2n+2}+\mu_{2n}-2\mu_{2n+1})$
色散关系： 将格波试解代入运动方程，可以得到两个频率解，对应于声学波和光学波两个分支：

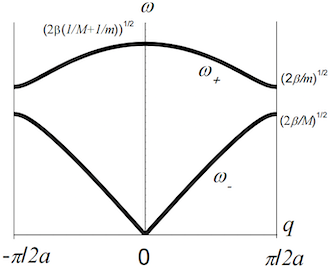
$w_{\pm}^2=\beta\frac{m+M}{mM}\left\{1\pm\left[1-\frac{4mM}{(m+M)^2}\sin^2(aq)\right]^{1/2}\right\}$
- 波数范围： 由于原胞变大，倒格矢变小，第一布里渊区也随之变小，波数 $q$ 的取值范围为 $-\pi/2a < q \le \pi/2a$ 。
- 格波数目： 对于双原子链，有 $2N$ 个原子，因此共有 $2N$ 个格波。
- 格波带隙： 在布里渊区边界 $q=\pi/2a$ 处，两个频率解分别为 $\sqrt{2\beta/m}$ 和 $\sqrt{2\beta/M}$ ，两者之差形成带隙。这两种振动模式在布里渊区边界发生布拉格反射，形成驻波。

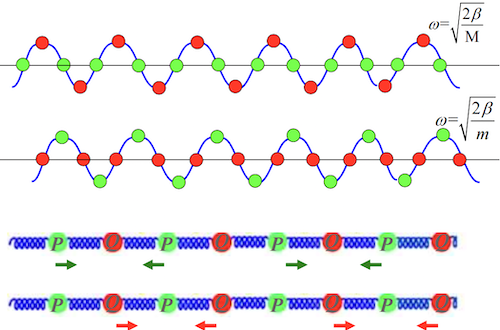
# 光学波与声学波

双原子链的两个频率分支被命名为光学波和声学波，其命名源于它们在长波极限（ $q\to0$ ）下的特性。

光学波（高频支 $w_+$ ）：
- 长波极限（ $q\to0$ ）： 频率最高，群速度为 0。
- 振动特征： 相邻原子振动方向相反，振幅与原子质量成反比，整个晶格的质心保持不变。
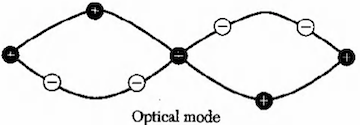
- 物理意义： 这种模式下，每个原胞内的不同原子做相对振动，产生电偶极矩，因此可以与电磁波相互作用，特别是在远红外光波段产生强烈吸收。
声学波（低频支 $w_-$ ）：
- 长波极限（ $q\to0$ ）： 频率正比于波数，群速度是一个常数。
- 振动特征： 相邻原子以相同的振幅和相位同步运动，整个原胞做整体运动。
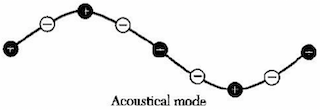
- 物理意义： 这类似于连续介质中的弹性波。任何晶体都存在声学波，但只有复式晶格结构（每个原胞含有多个原子）的晶体才存在光学波。

# 三维晶体中的格波

自由度与模式数： 若三维晶体有 $N$ 个原胞，每个原胞含 $n$ 个原子，则晶体的自由度为 $3nN$ 。格波的数目等于晶体的自由度数，即 $3nN$ 个振动模式。
格波分支： 这些振动模式可以分为 $3n$ 个分支，其中有 3 个声学分支（1个纵向声学波，2个横向声学波）和 $3(n-1)$ 个光学分支。
举例：
- 硅：晶格中虽然只有一种原子，但其是复式晶格结构，等同于有两个原子，因此存在声学波和光学波。
- 金属铅： 属于面心立方的简单晶格结构，没有光学波，只有三支声学波（不同方向上可能存在简并）。

# 准粒子与集体激发

# 极化激元（Polaritons）

光子与光学模声子之间的耦合模式被称为极化激元。当光照射离子晶体时，会激发横向电磁场，影响光学波振动，导致光子与声子的色散关系曲线发生显著改变，形成新的耦合模式。

其他例子： 等离子振荡、激子、自旋波等也存在类似的耦合现象，统称为极化激元。

# 元激发与准粒子

固体中的元激发可以分为两类：

集体激发的准粒子：
- 声子： 晶格振动的格波是最典型的集体激发，其准粒子为声子。它表示所有原子的一种集体运动。
- 磁振子： 自旋波是另一个集体激发的例子，其准粒子是磁振子。
单粒子激发的准粒子：
- 准电子： 金属中的电子可以理解为单粒子激发的准粒子。它将电子和周围的屏蔽电荷云视为一个整体，构成准电子，其有效质量与原始电子不同，但数目相同，并服从费米统计。