9. 霍尔效应

# 霍尔效应简介

当电流垂直于外部磁场通过导体时，在垂直于电流和磁场方向的两个侧面之间会产生一个电势差，这个现象被称为霍尔效应。该电势差称为霍尔电压。

---

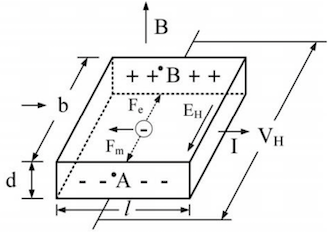
# 霍尔电压与霍尔电场

在霍尔效应中，磁场对运动电荷施加洛伦兹力，从而在导体内部产生一个电场，即霍尔电场 $E_H$。该电场对电荷的电场力与洛伦兹力大小相等、方向相反，达到动态平衡。

• 对于电子（带负电）：

  • 洛伦兹力：$F_L = qv_x B_z = -ev_x B_z$
  • 霍尔电场力：$F_E = qE_H = -eE_H$
  • 平衡时：$F_L + F_E = 0 \Rightarrow -ev_x B_z - eE_H = 0 \Rightarrow E_H = -v_x B_z$
  • 电流密度：$j_x = -nev_x$
  • 霍尔电场：$E_H = -\frac{j_x B_z}{ne}$

• 对于空穴（带正电）：

  • 洛伦兹力：$F_L = qv_x B_z = +ev_x B_z$
  • 霍尔电场力：$F_E = qE_H = +eE_H$
  • 平衡时：$F_L + F_E = 0 \Rightarrow +ev_x B_z + eE_H = 0 \Rightarrow E_H = -v_x B_z$
  • 电流密度：$j_x = pev_x$
  • 霍尔电场：$E_H = -\frac{j_x B_z}{pe}$

霍尔电场的方向可以用来判断导电载流子的类型，而其数值可用于计算载流子浓度。

---

# 霍尔系数与霍尔电阻

霍尔系数 $R_H$ 是描述霍尔效应大小的关键物理量，定义为霍尔电场与电流密度和磁场强度的比值。

$R_H = \frac{E_H}{j_x B_z}$

• 对于电子：$R_H = -\frac{1}{ne}$
• 对于空穴：$R_H = \frac{1}{pe}$

霍尔电压 $V_y$ 是指在导体宽度为 $b$ 的方向上产生的电势差。

$V_y = E_H b$

将 $j_x = I_x / (bd)$ 代入霍尔电场表达式，可得：

$V_y = R_H \frac{I_x}{bd} B_z b = R_H \frac{I_x B_z}{d}$

其中，$d$ 为样品厚度，$I_x$ 为通过样品的电流。

霍尔电阻 $R_{xy}$ 定义为霍尔电压与电流的比值。

$R_{xy} = \frac{V_y}{I_x} = \frac{R_H B_z}{d}$

---

# 霍尔电导

霍尔电导 $\sigma_{xy}$ 是在霍尔效应中，电场 $E_y$ 和电流密度 $j_x$ 的比值。

$j_x = \sigma_{xy} E_y$

则 $\sigma_{xy} = \frac{j_x}{E_y} = \frac{j_x}{E_H} = \frac{j_x}{j_x R_H B_z} = \frac{1}{R_H B_z}$

• 对于电子：$\sigma_{xy} = \frac{1}{-\frac{1}{ne} B_z} = -\frac{ne}{B_z}$
• 对于空穴：$\sigma_{xy} = \frac{1}{\frac{1}{pe} B_z} = \frac{pe}{B_z}$