7. 半导体载流子输运过程

# 半导体器件基础

# 半导体电子器件

二极管：
- 类型：金属-半导体二极管、半导体PN结二极管。
- 应用：整流、混频。
晶体管（三极管）：
- 类型：半导体晶体管、金属-氧化物-半导体场效应管（MOSFET）。
- 应用：交流信号放大。
集成电路：
- 特点：在同一芯片内集成无数个晶体管、电阻、电容等。
- 应用：广泛应用于计算机、手机等领域，无所不在。

# 半导体光子器件

光学吸收：
- 太阳能电池：将光能转化为电能，作为电源给负载供电。主要以硅（Si）材料为主。
- 光电探测器：将光信号转换为电信号。常用材料包括Si、锗（Ge）、砷化铟镓（InGaAs）。
产生光信号：
- 发光二极管（LED）：将电流转化为光。
  - 可见光：用于照明、显示。
  - 红外光：用于低速率通信、遥控。
- 激光二极管（LD）：将电流转化为激光。
  - 特点：产生的光子具有很好的单色性、相干性和方向性。
  - 应用：高速光通信、光存储、激光测距等。
- 材料：砷化镓（GaAs）、磷化铟（InP）、氮化镓（GaN）等。探索Si材料发光是重要研究方向。

# 载流子浓度与费米能级

# 半导体的能带模型

能带结构：最高的满带（价带）的电子容易被激发到上面的空带（导带）。
载流子：导带中的电子和价带中的空穴。
禁带：导带和价带之间的能量间隙，其宽度 $E_g$ 一般小于 2 eV。

# 状态密度

自由电子：
$g(E)=\frac{V}{2\pi^2}\left(\frac{2m}{\hbar^2}\right)^{3/2}E^{1/2}$
半导体电子、空穴：
$g(E)=\frac{V}{2\pi^2}\left(\frac{2m^*}{\hbar^2}\right)^{3/2}\Delta E^{1/2}$
其中 $\Delta E$ 是与导带底或价带顶的能量差， $m^*$ 为有效质量。

# 半导体中载流子的费米统计分布

导带底电子的能态密度：
$N_-(E)=\frac{4\pi(2m_-^*)^{3/2}}{h^3}\sqrt{E-E_-}$
其中 $E_->E_F$ 是导带底的能量。
价带顶空穴的能态密度：
$N_+(E)=\frac{4\pi(2m_+^*)^{3/2}}{h^3}\sqrt{E_+-E}$
其中 $E_+<E_F$ 是价带顶的能量。

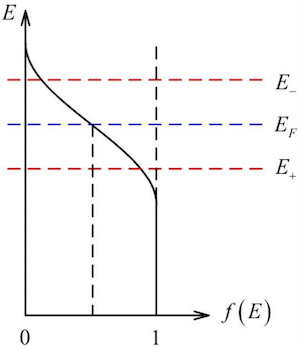
# 电子和空穴的浓度

电子浓度 ( $n$ )：
$n=\int_{E_-}^\infty f(E)N_-(E)dE = N_-e^{-(E_--E_F)/k_BT}$
其中 $N_-$ 为导带电子有效能级密度，定义为：
$N_-=\frac{2(2\pi m_-^*k_BT)^{3/2}}{h^3}$
空穴浓度 ( $p$ )：
$p=\int_{-\infty}^{E_+}(1-f(E))N_+(E)dE = N_+e^{-(E_F-E_+)/k_BT}$
其中 $N_+$ 为价带空穴有效能级密度，定义为：
$N_+=\frac{2(2\pi m_+^*k_BT)^{3/2}}{h^3}$
有效能级密度概念：在计算载流子浓度时，可以等效地用导带底能级 $E_-$ 和价带顶能级 $E_+$ 代替整个能带，载流子数就如同在导带底和价带顶处分别集中了 $N_-$ 和 $N_+$ 个能态所含有的载流子数。

# 两种载流子浓度的乘积

公式：
$np = N_-N_+\exp\left(-\frac{E_g}{k_BT}\right) = n_i^2$
特点：在热平衡时，半导体中两种载流子浓度的乘积是一个仅与禁带宽度 $E_g$ 及温度 $T$ 有关的量，而与费米能级 $E_F$ 无关。

# 本征半导体

# 定义与特点

定义：不含任何杂质及缺陷的半导体。
载流子：电子受热激发，从价带跃迁到导带，在导带产生电子，同时在价带留下空穴。
载流子浓度：电子数目等于空穴数目，统称本征载流子。其浓度 $n_i$ 完全取决于半导体本身的性质。

# 本征载流子浓度与费米能级

本征载流子浓度 ( $n_i$ )：
$n_i = n = p = (N_-N_+)^{1/2}\exp\left(-\frac{E_g}{2k_BT}\right)$
- 随温度升高而呈指数增加。
- 与带隙宽度有关，带隙越小，浓度越高。
本征费米能级 ( $E_{Fi}$ )：
$E_{Fi} = \frac{E_-+E_+}{2} + \frac{3}{4}k_BT\ln\left(\frac{m_+^*}{m_-^*}\right)$
- 在一般情况下，由于 $k_BT$ 较小且 $m_h^*$ 与 $m_e^*$ 相差不大，本征半导体的费米能级 $E_{Fi}$ 近似地位于带隙的中间。

# 杂质与杂质激发

# 非简并半导体

杂质能级：半导体中的杂质或缺陷（如空位、间隙原子、位错）会破坏严格的周期性势场，从而在带隙中产生局域化的电子态——杂质能级。
非简并条件：杂质浓度远小于半导体原子浓度，施主电子或受主空穴之间不存在相互作用，杂质在半导体中引入分离的杂质能级。

# 施主杂质

定义：杂质在能隙中提供带有电子的能级，其束缚能（电离能） $E_i = E_--E_D$ 很小。
类型：如在Si或Ge中掺入五价元素（P, As, Sb）形成N型半导体。
导电机制：电子由施主能级激发到导带远比价带激发容易，N型导电几乎完全依靠施主热激发到导带的电子。

# 受主杂质

定义：杂质提供带隙中空的能级，其束缚能（电离能） $E_i = E_A-E_+$ 很小。
类型：如在Si或Ge中掺入三价元素（B, Al, In）形成P型半导体。
导电机制：电子由价带激发到受主能级比激发到导带容易，P型导电几乎完全依靠受主热激发到导带的空穴。

# 浅能级与深能级杂质

浅能级杂质：能级靠近导带或价带，其对电子或空穴的束缚能很小，载流子将以杂质跃迁产生为主。
深能级杂质：能级位于禁带中部，通常为多重能级，如Au在Si中。它们是有效的复合中心，会降低载流子寿命，也可作为补偿杂质提高材料电阻率。

# 载流子浓度与费米能级

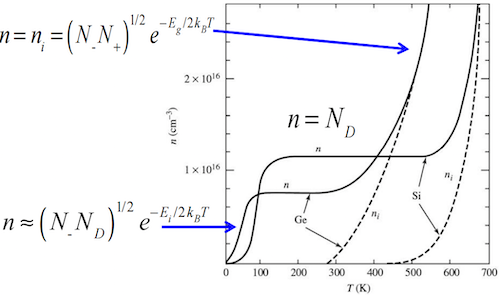
N型半导体：
- 多数载流子（电子）浓度 ( $n$ )：
  - 低温时： $n \approx (N_-N_D)^{1/2}e^{-E_i/2k_BT}$ ，随温度指数增加。
  - 高温时： $n \approx N_D$ ，施主几乎全部电离激发。
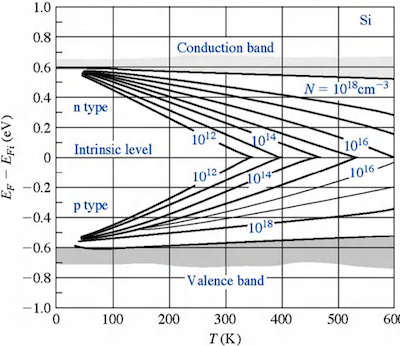
- 费米能级 ( $E_F$ )： $E_F = E_{Fi} + k_BT\ln(n/n_i)$ 。掺杂浓度越高，费米能级越靠近导带。
P型半导体：
- 多数载流子（空穴）浓度 ( $p$ )：
  - 低温时： $p \approx (N_AN_+)^{1/2}e^{-E_i/2k_BT}$ 。
  - 高温时： $p \approx N_A$ 。
- 费米能级 ( $E_F$ )： $E_F = E_{Fi} - k_BT\ln(p/n_i)$ 。掺杂浓度越高，费米能级越靠近价带。
少数载流子浓度：在非本征半导体中，少数载流子浓度可由 $n_i^2=np$ 关系得到。

# 简并半导体

定义：当杂质浓度非常高，以至于杂质原子之间相互作用加强，分离的杂质能级分裂并展宽形成能带，费米能级进入导带或价带。
费米统计：此时玻尔兹曼分布近似不再适用，必须使用费米-狄拉克分布来计算载流子浓度。

# 补偿半导体

定义：在半导体中既掺有施主又掺有受主的半导体。
载流子浓度：在完全电离条件下，载流子浓度由施主和受主浓度的差值决定。
- N型补偿半导体：当 $N_D > N_A$ ，电子浓度 $n \approx N_D - N_A$ 。
- P型补偿半导体：当 $N_A > N_D$ ，空穴浓度 $p \approx N_A - N_D$ 。
特性：由于杂质的补偿作用，有效载流子浓度很小，因此补偿半导体的电阻率很高。

# 载流子的迁移

# 迁移率与电导率

迁移率 ( $\mu$ )：定义为单位电场下载流子的平均漂移速度。
电导率 ( $\sigma$ )：
$\sigma = nq\mu_- + pq\mu_+$
其中 $\mu_-$ 和 $\mu_+$ 分别是电子和空穴的迁移率。
欧姆定律：电流密度 $j = \sigma E$ 。
迁移率公式： $\mu=\frac{q\tau}{m^*}$ ，其中 $\tau$ 为平均弛豫时间。

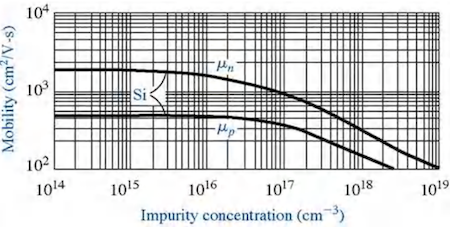
# 迁移率的影响因素

温度：
- 低温：主要受杂质散射影响。温度升高，杂质散射作用减弱，迁移率增大， $\mu \propto T^{3/2}$ 。
- 高温：主要受晶格散射影响。温度升高，晶格振动增强，散射作用增大，迁移率下降， $\mu \propto T^{-3/2}$ 。
掺杂浓度：载流子的迁移率由总的掺杂浓度决定。掺杂浓度越高，杂质散射越强，迁移率越低。

# 半导体的电导率特性

电导率随温度变化：除了饱和区外，电导率随温度升高呈指数形式迅速增大，表现出很强的热敏性。
与金属的比较：
- 金属：载流子浓度几乎不变，电导率主要由迁移率决定，而迁移率随温度升高而减小，故金属电导率随温度升高而下降。
- 半导体：载流子浓度随温度呈指数变化，是决定电导率的主要因素，因此电导率随温度升高而迅速增大。