4. 布洛赫电子

# 布洛赫定理

# 周期性势场下的电子运动

在晶体中，电子受到周期性势场 $V(\vec{r}) = V(\vec{r}+\vec{R}_n)$ 的作用，其中 $\vec{R}_n$ 是晶格原胞的平移矢量。根据布洛赫定理，在这样的势场中运动的电子的波函数 $\psi(\vec{r})$ 具有以下形式：

$$\psi(\vec{r}) = e^{i\vec{k}\cdot\vec{r}}u(\vec{r})$$

其中，$u(\vec{r})$ 是一个与晶格具有相同周期性的函数，即 $u(\vec{r}+\vec{R}_n) = u(\vec{r})$；$\vec{k}$ 称为波矢。

布洛赫定理的另一种表述为：

$$\psi(\vec{r}+\vec{R}_n) = e^{i\vec{k}\cdot\vec{R}_n}\psi(\vec{r})$$

这个表达式表明，在周期性势场中，相邻原胞中相应位置的波函数之间仅相差一个相位因子 $e^{i\vec{k}\cdot\vec{R}_n}$。

在实际计算中，通常使用周期性边界条件（Born-von Karman条件）来处理无限晶体：$\psi(x+Na) = \psi(x)$。这使得波矢 $k$ 的取值离散化：$k = \frac{2\pi n}{L}$，其中 $L = Na$ 是晶体长度。

# 特征根方法求解周期性势场

求解周期性势场中电子的不含时薛定谔方程：

$$\left[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V(x)\right]\psi(x) = E\psi(x)$$

由于势场 $V(x)$ 和波函数 $\psi(x)$ 都是周期性的，可以将它们进行傅里叶级数展开：

$$V(x) = \sum_n V_n\exp(i\frac{2\pi}{a}nx) \\ \psi(x) = e^{ikx}u(x),~u(x) = \sum_n u_n\exp(i\frac{2\pi}{a}nx)$$

将这些展开式代入薛定谔方程，并利用波函数的正交归一性，最终可得到一个关于 $u_n$ 的线性方程组。该方程组的系数矩阵 $A$ 的行列式必须为零才有非平凡解：

$$A = \begin{bmatrix} \cdots&\cdots&\cdots&\\ \frac{\hbar^2}{2m}\left(k-\frac{2\pi}{a}\right)^2-E+V_0&V_{-1}&V_{-2}&\\ V_1&\frac{\hbar^2}{2m}k^2-E+V_0&V_{-1}&\\ V_2&V_1&\frac{\hbar^2}{2m}\left(k+\frac{2\pi}{a}\right)^2-E+V_0&\\ \cdots&\cdots&\cdots&\vdots \end{bmatrix}\\ \det A = 0$$

给定波矢 $k$，这个行列式方程可以解出多个能量本征值 $E$，这些能量值构成了晶体中的能带。

# 布里渊区

• 简约波矢与第一布里渊区

  • 通过对波函数进行平移，可以发现波矢 $k' = k + 2\pi j/a$ 对应的波函数 $\psi_{k'}$ 与波矢 $k$ 对应的波函数 $\psi_k$ 具有相同的平移相位关系。
  • 这表明可以将波矢 $k$ 的取值范围限制在 $-\frac{\pi}{a} \le k \le \frac{\pi}{a}$ 内，这个范围称为第一布里渊区。在此区域内，每个 $k$ 值都对应一个独特的物理状态。
  • 事实上，特征根方法在任意布里渊区内求解所得的能量本征值都是相同的，因此我们只需要研究第一布里渊区内的 $k$ 值。

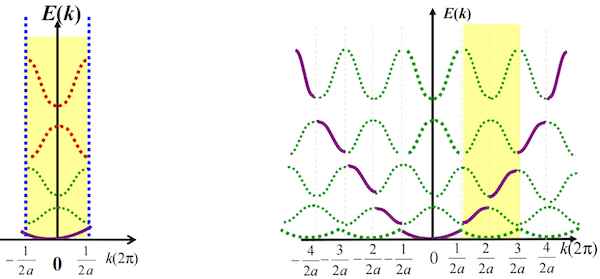
• 周期布里渊区

  • 通过将第一布里渊区周期性平移，可以得到所有布里渊区。
  • 在周期布里渊区图景中，能量 $E$ 随 $k$ 的绝对值单调递增，每条曲线代表一个独立的能带。

---

# 近自由电子近似

近自由电子近似（弱晶格近似）将晶体中的电子视为在周期性势场下受到微扰的自由电子。

# 零级微扰

在零级近似下，势场 $V(x)$ 被其平均值 $\overline{V}$ 所取代。此时的哈密顿量 $H_0 = -\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+\overline{V}$ 描述的是自由电子。

其零级能量本征值和本征函数分别为：

$$E_k^{(0)} = \frac{\hbar^2k^2}{2m}+\overline{V} \\ \psi_k^{(0)} = \frac{1}{\sqrt{L}}e^{ikx}$$

# 二级微扰

一阶能量修正 $E_k^{(1)} = \int \psi_k^{(0)*}H'\psi_k^{(0)}dx = \int \psi_k^{(0)*}(V(x)-\overline{V})\psi_k^{(0)}dx = 0$。

二阶能量修正为：

$$E_k^{(2)} = \sum_{k'\ne k}\frac{|\langle k'|\Delta V|k\rangle|^2}{E_k^{(0)}-E_{k'}^{(0)}}$$

其中，$\langle k'|\Delta V|k\rangle$ 只有在 $k' = k + \frac{2\pi n}{a}$ 时不为零，其值为 $V_n$。因此，二阶能量修正可简化为：

$$E_k^{(2)} = \sum_{n\ne0}\frac{|V_n|^2}{\frac{\hbar^2}{2m}\left[k^2-\left(k+\frac{2\pi}{a}n\right)^2\right]}$$

最终的波函数是零级波函数与一级修正的叠加：

$$\psi_k = \frac{1}{\sqrt{L}}e^{ikx}\left\{ 1+\sum_{n\ne0}\frac{V_n}{\frac{\hbar^2}{2m}\left[k^2-\left(k+\frac{2\pi}{a}n\right)^2\right]}\cdot\exp(i\frac{2\pi}{a}nx)\right\} = \frac{1}{\sqrt{L}}e^{ikx}u(x)$$

这个结果的物理含义是，周期场中的电子波函数是波矢为 $k$ 的前进平面波与被周期势场散射的各散射波叠加而形成的调幅平面波。平面波因子 $e^{ikx}$ 描述了电子在整个晶体中的共有化运动，而周期函数 $u(x)$ 则反映了电子在单个原胞内的周期性运动。

# 简并二级微扰与带隙的产生

当电子波矢 $k$ 接近布里渊区边界时，例如 $k=\frac{\pi n}{a}$，此时 $E_k^{(0)} \approx E_{k'}^{(0)}$，即零级能量发生简并，常规微扰方法失效。此时，简并二级微扰处理更为准确。

零级近似波函数应选择简并态的线性组合：$\psi = a\psi_k^{(0)} + b\psi_{k'}^{(0)}$。代入薛定谔方程，可以得到一个关于能量 $E$ 的久期方程：

$$\det A = \left|\begin{matrix} E_k^{(0)}-E&V_n^*\\ V_n&E_{k^{\prime}}^{(0)}-E \end{matrix}\right|=0$$

解得两个能量本征值：

$$E_\pm = \frac{1}{2}\left\{(E_k^{(0)}+E_{k'}^{(0)})\pm\left[(E_k^{(0)}-E_{k'}^{(0)})^2+4|V_n|^2\right]^{1/2}\right\}$$

• 在布里渊区边界上，即 $E_k^{(0)}=E_{k'}^{(0)}=E^{(0)}$，能量的解为 $E_\pm = E^{(0)} \pm |V_n|$。这导致了两个能量分支之间出现一个带隙，其宽度为 $2|V_n|$。

• 在远离布里渊区处，即 $|E_k^{(0)}-E_{k'}^{(0)}|\gg |V_n|$，解近似于 $E_k^{(0)}$ 和 $E_{k'}^{(0)}$，能带曲线接近自由电子的抛物线。

# 能带与带隙的本质

能带是由于晶体中电子的共有化运动而形成的，当晶体中的原胞数目 $N$ 很大时，每个能带内包含的能级变得非常密集，形成准连续状态。

带隙的出现是周期性势场的直接结果。在简并处，电子的驻波态被分为两种，一种电荷密度主要集中在正离子处，另一种电荷密度主要集中在正离子之间，这两种驻波态具有不同的能量，从而在能带之间产生了能量禁带。

---

# 布里渊区图景

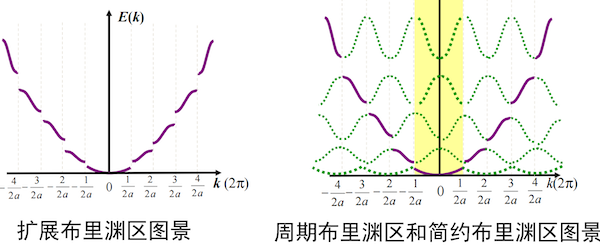
不同的布里渊区图景只是描述方式不同，其物理本质是相同的。

• 扩展布里渊区图景：波矢 $k$ 的取值范围为 $(-\infty, +\infty)$，直接代表了前进平面波的动量。

  • 属于不同布里渊区的能级对应不同的能带，能在布里渊区边界发生突变。

• 简约布里渊区图景：波矢 $k$ 局限在第一布里渊区 $[-\frac{\pi}{a}, \frac{\pi}{a}]$ 内。

  • 波矢 $k$ 只代表相邻原胞间的波函数相位关系。
  • 对于每一个简约波矢 $k$ 都有多个能量本征值，每个值对应一个能带。因此，指明一个电子状态需要同时确定简约波矢和其所属的能带。

• 周期布里渊区图景：能带曲线由第一布里渊区的能带曲线进行周期性平移得到。这种图景清晰地展示了能带的周期性特征。