# 晶体的结构
# 晶体的概念与基本特征
-
晶体的概念: 晶体是原子排列具有空间周期性的固体。这种周期性是晶体最基本的特征。
-
晶体的基本特征: 晶体具有以下几个显著特征:
- 规则的几何外形: 具有对称、规则的外观。
- 固定的熔点: 在特定温度下由固态转变为液态。
- 晶面角守恒: 同一物质的晶体,在相同条件下,晶面夹角保持不变。
- 物理性质的各向异性: 物理性质(如导热性、折射率)在不同方向上表现不同。
-
多晶体与单晶体:
- 单晶体是由单一晶粒组成的晶体。
- 多晶体由许多单晶粒随机排列组合而成。
- 多晶体的单晶粒之间没有固定的周期性,但每个单晶粒的内部都具有点阵式的周期性结构。
-
对理想晶体的假设:
- 为了方便研究,我们通常假设完美的晶体是无穷大的单晶体。
- 然而,现实世界中不存在完美的晶体,因为总会存在表面、原子振动以及各种缺陷。
- 在研究中,我们通常假设固体表面、原子振动和缺陷对固体性质的影响很小,可以忽略不计。
# 晶格与晶胞
-
晶格/点阵(Lattice):
- 为了描述晶体及其周期性,我们将晶体中的原子(或原子团)抽象成一个点,将这些点连接起来便构成了规则排列的格架。
- 每一个格点被称为基元(Basis),可以是一个原子或一个原子团。
- 晶格/点阵是格点排布成的几何图形,它具有与晶体相同的几何特性,但本身没有物理实质。
- 晶体结构 = 晶格(点阵)+ 基元。
-
晶胞与原胞:
- **晶胞(Cell)**是晶格的周期性重复单元。
- 原胞是体积最小的晶胞,是可完全平移覆盖点阵的最小单元。一个原胞只包含一个格点。
- 任意格点的位矢 可以表示为:
其中, 是原矢,它们是格点间平移矢量的基矢,也称为晶格基矢。
-
单胞(惯用晶胞):
- 单胞是晶体学中规定的周期性单元,通常根据晶体的对称性来选取,通常是能够最直观体现晶体对称性的最小单元。
- 晶格常数是惯用晶胞的边长。
- 不同晶格的惯用原胞基矢:
- 简单立方:
- 体心立方:
- 面心立方:
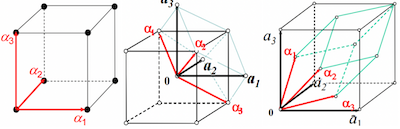
- 简单立方:
# 晶格分类与重要结构
-
布拉菲点阵(Bravais Lattices):
- 根据对称性对三维点阵进行分类,结果表明三维空间点阵只能有十四种,分别属于七个晶系。
-
简单晶格和复式晶格:
- 简单晶格: 所有原子是完全等价的,化学性质相同且在晶格中处于完全相同的地位。每个格点代表一个原子。
- 复式晶格: 原子之间不等价,可能是不同化学元素或空间几何构形。每个格点对应多个原子。例如体心立方、面心立方闪锌矿结构和金刚石结构等。复式晶格可被视为由多个简单晶格相互穿套而成。
-
几种重要的晶体结构:
- 简单立方晶格(Simple Cubic): 属于立方晶系,如。几乎没有其他实际晶体的原子排布是简单立方结构。
- 体心立方晶格(Body-Centered Cubic, BCC): 属于立方晶系,如等碱金属。
- 面心立方晶格(Face-Centered Cubic, FCC): 属于立方晶系,如等金属元素。
- 六角密排晶格(Hexagonal Close-Packed, HCP): 属于六角晶系,如等金属。
- 金刚石结构: 由面心立方单元的中心向顶角引8条对角线,在其中互不相邻的4条对角线的中点各加一个格点。每个原子有四个最近邻原子,正好位于一个正四面体的顶角位置。例如硅、锗。
- 闪锌矿结构: 例如。
- 纤锌矿结构: 例如。
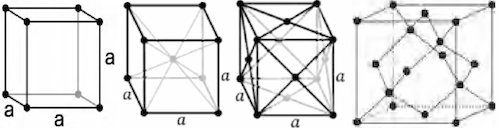
-
密堆排列结构:
- A层:密堆面,每个原子周围有6个原子。
- B位:倒三角形空隙。
- C位:正三角形空隙。
- 面心立方是ABC堆积:第二层相对第一层在B位,第三层相对第二层在B位(但相对第一层在C位),第四层与第一层空间位置一致,形成**ABC ABC...**重复。
- 六角密排是AB堆积:第二层相对第一层在B位,第三层与第一层空间位置一致,形成**AB AB...**重复。
- 堆积比是原子体积占总体积的百分数。
# 晶体的方向性与对称性
-
描述晶面的方向性:
- 晶列是晶格构成的一组平行直线,其方向被称为晶向。
- 晶向指数:采用惯用晶胞为参考系,由位矢 确定。负向指数在数字上方加横杠,如。
- 等效晶向:具有相同性质且对称的晶向。
- 晶面是晶格构成的一组平行等距的平面系。
- 晶面族一经划定,所有格点均被包含在内,其中必有一个晶面通过原点。
- 同一晶格可以有无数方向不同的晶面系。
- 密勒指数:采用惯用晶胞为参考系,是第一个离开原点的晶面与单胞基矢轴截距倒数的最小整数比。
- 等效晶面:晶面间距和原子分布完全相同,但空间位向不同的晶面。
- 晶列是晶格构成的一组平行直线,其方向被称为晶向。
-
晶格的对称性:
- 对称变换是指经过某一正交变换后,整个点阵保持不变。
- 晶格的基本对称变换只有平移、旋转和镜反射三种,它们可以组合成更复杂的对称变换。
- 对称素是对称操作的实体表现,例如对称轴、对称面。
- 点群是由对称素组成的对称操作群。
- 晶格的根本特性是有限的平移对称性(旋转对称性也是有限的)。
# 倒易点阵与布里渊区
# 晶体结构的观测与衍射
- 晶格衍射: 晶体结构的观测手段主要依赖于晶格衍射。自然界中存在三种波:电磁波、物质波和机械波。
- 倒易点阵由厄瓦尔为解释X射线衍射而提出。
- 布里渊区由布里渊为研究晶体中电子运动而提出。
- 劳厄衍射方程: 忽略具体的散射物理机制,仅讨论不同格点处散射波之间的干涉。
- 衍射极大条件:
- 劳厄衍射方程:
其中, 是晶格中任一格点的位矢; 和 分别是入射光和散射光的波矢。
# 倒格矢与倒易点阵
- 倒格矢(Reciprocal Lattice Vector):
- 由于晶格的周期性,其相关物理性质也为周期函数。
- 倒格矢是满足 的波矢,。
- 倒格子是倒易(波矢)空间的格子,是所有端点的集合。
- 倒格子的求法:
- 倒格子基矢与晶格基矢满足关系。
- 三维解:
- 常用晶格的倒格子:
- 简单立方的倒格子为简单立方。
- 体心立方的倒格子为面心立方。
- 面心立方的倒格子为体心立方。
# 倒格子与衍射定律
- 倒格子与晶面系: 倒格矢垂直于对应的正格子晶面系,且其模长,其中为晶面间距。
- 倒格子与XRD:
- 劳厄衍射方程可表示为 ,表明晶格周期性使得实际波与以倒格矢为波矢的波之间发生作用。
- 考虑弹性散射(),可推导出布拉格定律: ()。
- XRD实际测量的是衍射角,XRD谱上的一个斑点与正格子的一族晶面对应,晶体衍射图样是晶体倒格子的映像。
- 要发生衍射,波长必须小于。
# 布里渊区与其他衍射
- 布里渊区(Brillouin Zone):
- 在倒格子空间中,以某倒格点为中心,由该中心格点到相邻格点的连线的垂直平分面所围成的多面体。
- 第一布里渊区是倒易点阵中的W-S原胞。
- 只有当入射波矢由布里渊区边界指向倒格点时才能发生XRD。
- 常用晶格的第一布里渊区: 简单立方是正方体;面心立方是14面体;体心立方是12面体。
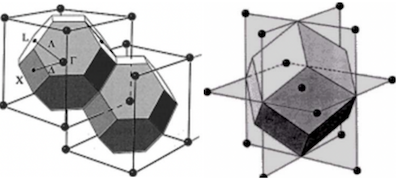
- 其他实物粒子衍射:
- 电子衍射: 电子对原子的散射截面大,衍射强度高,测量速度快,易实现短波长。
- 中子衍射: 中子与原子核之间有强相互作用,与电子无相互作用。中子衍射可区分同位素并探测各种准粒子,尤其对轻原子有良好衍射图像,但需要核反应堆,检测困难,亮度低,实验时间长。
# 无序固体的结构
- 非晶体(Amorphous Solids):
- 组成物质的分子、原子或离子不呈空间周期性排列的固体。
- 没有规则的外形,如玻璃、松香、石蜡等。
- 物理性质表现为各向同性,在各个方向上相同。
- 没有固定的熔点,可被视为“过冷液体”或“流动性很小的液体”。
- 非晶态固体分类: 非晶态电介质、非晶态半导体、非晶态金属。
- 准晶体(Quasicrystals):
- 具有长程取向序,但无长程平移序。
- 取向序具有晶体周期性所不允许的点群对称性。
- 沿取向序对称轴方向具有准周期性,即具有两个或两个以上不可公度的特征长度。
# 晶体中的缺陷与扩散
- 晶体缺陷: 晶体结构中任何偏离理想点阵周期性的部分都被称为晶体缺陷。
- 面缺陷: 多晶体晶粒之间的交界区(晶粒间界)可视为一种晶体缺陷。纳米材料因其大的界面积和界面原子排列的混乱,在外力作用下原子易于迁移,表现出优良的韧性和延展性。
- 线缺陷: 晶体中某处有一列或若干列原子发生有规律的错排现象。最常见的线缺陷是位错,它是晶体内部局部滑移造成的。
- 螺型位错:位错线与滑移方向平行。
- 刃型位错:位错线与滑移方向垂直。
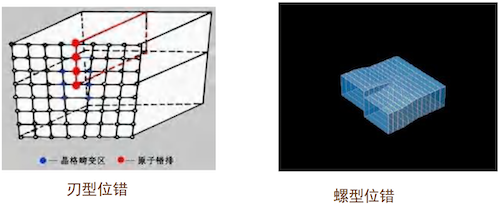
- 点缺陷: 晶格中某个原子脱离平衡位置形成的空位,或某个晶格间隙挤进原子形成的间隙原子。离子晶体中的点缺陷通常带有电荷。
- 晶体中的扩散:
- 扩散是原子无规则布朗运动的体现。
- 在固态中,物理和化学变化常通过扩散进行。
- 晶体中的扩散受到晶格周期性的限制,原子需要克服势垒才能实现跳跃。对于简单晶格,缺陷每跳一步的间距等于跳跃方向上的周期。
- 晶体中的扩散过程与微观缺陷密切相关。