4. 基带调制

# 概述与基本概念

基带调制是一种将数字信息转换为适合在基带信道上传输的电信号的技术。它通过不同的电平或脉冲形状来表示数字比特。

与采样（如$m(t)=\sum_nm(nT_s)\frac{sin[2\pi W(t-nT_s)]}{2\pi W(t-nT_s)}$）不同，基带调制信号通常表示为脉冲序列的线性叠加：$s(t)=\sum_k s_k\phi_k(t)$。

# 符号（Symbol）与比特（Bit）

• 符号：一个符号可以携带多个比特的信息。
• M：符号集合的大小。
• r：每个符号携带的比特数，$r=\log_2M$。
• 调制方式：
  • 幅移键控（ASK） 和 脉冲幅度调制（PAM）：通过改变脉冲幅度来表示不同的符号。
  • 频移键控（PSK） 和 正交幅度调制（QAM）：虽然属于带通调制，但其原理与基带调制密切相关。
• 格雷码：一种编码方式，用于在相邻符号间只改变一个比特，以减少误码代价。

# 基带调制过程

基带调制通常使用相同的脉冲波形来表示所有符号：

$$s(t)=\sum_ks_kg(t-kT_s)$$

其中，$g(t)$ 是脉冲波形，$s_k$ 是符号序列。

# 速率与信道

• 符号率（Symbol rate）：$R_s=\frac1{T_s}$。
• 比特率（Bit rate）：$R_b=R_s\log_2 M=\frac1{T_s}\log_2 M$。
• 信道特点：基带信道通常是频带受限的。为了满足这一要求，脉冲波形 $g(t)$ 的频谱 $G(f)$ 必须是带限的。

---

# 奈奎斯特准则（Nyquist Criterion）

# 码间串扰（ISI）

• 目的：在接收端，需要从叠加信号 $s(t)$ 中恢复出原始符号序列 $s_k$。
• 问题：如果脉冲波形重叠，接收到的信号在采样时刻会受到前后符号的干扰，这就是码间串扰（ISI）。

$$s(nT_s)=s_ng(0)+\sum_{k\ne n}s_kg((n-k)T_s)$$

• 消除 ISI：为了在采样时刻 $t=nT_s$ 消除 ISI，需要满足以下条件：

  $$ISI=\sum_{k\ne n}s_kg((n-k)T_s)=0$$

  $$g(0)=1$$

  这样，$s(nT_s)=s_n$，即可无失真地恢复符号。

# 奈奎斯特第一准则

• 时域条件：脉冲波形 $g(t)$ 必须在所有非零采样时刻为零。

$$g(kT_s)=I_{k=0} \quad (\text{其中 }I \text{是指示函数})$$

• 频域条件：脉冲频谱 $G(f)$ 在频移 $nf_s$ 后的周期延拓之和为一个常数。

$$\sum_n G(f-nf_s)=T_s=const$$

• 奈奎斯特带宽：根据奈奎斯特准则，无 ISI 传输所需的最小带宽为 $W_{min}=R_s/2$。
• 速率与带宽：

  $$R_s\le 2W$$

  $$R_b\le 2W\log_2M$$

• 带宽效率：

  $$\eta=\frac{R_b}W\le 2\log_2M$$

---

# 升余弦滤波器（Raised Cosine Filter）

升余弦滤波器是一种在满足奈奎斯特准则的同时，兼顾时域波形衰减速度的常用滤波器。

• 频域表达式：

  $$G_{rc}(f) = \begin{cases} T_s & |f| \le \frac{1-\alpha}{2T_s} \\ \frac{T_s}{2}\left[1+\cos\left(\frac{\pi T_s}{\alpha}\left(|f|-\frac{1-\alpha}{2T_s}\right)\right)\right] & \frac{1-\alpha}{2T_s} < |f| \le \frac{1+\alpha}{2T_s} \\ 0 & |f| > \frac{1+\alpha}{2T_s} \end{cases}$$

  其中，$T_s$ 是符号周期。
• 频域图像：
  
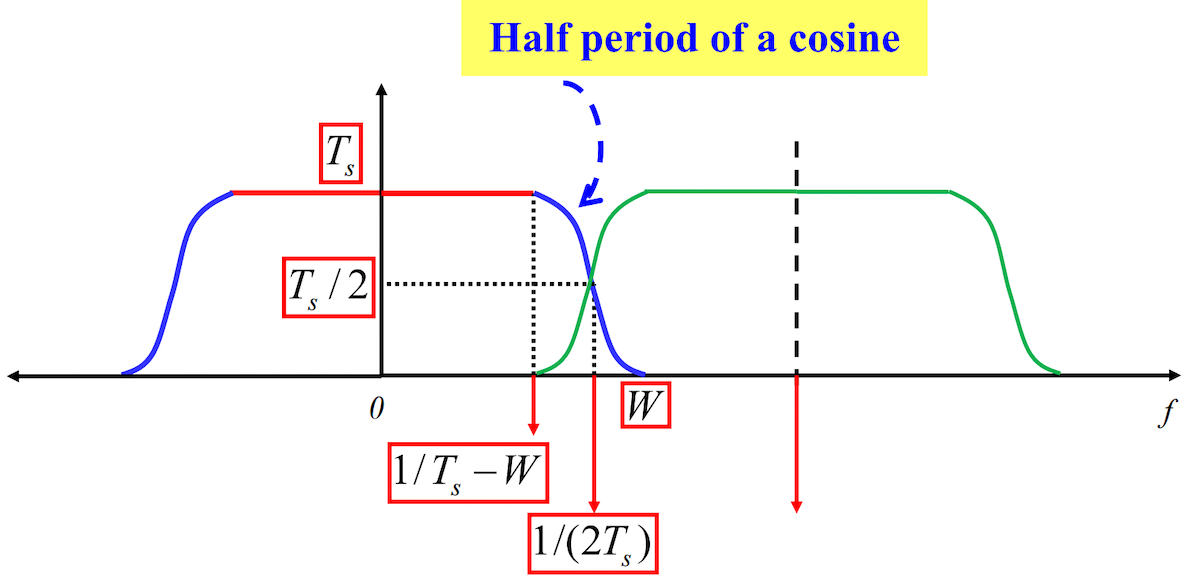
• 滚降系数（Rolloff factor）：$\alpha$ 是一个介于 0 到 1 之间的值，用于控制滤波器的过渡带。

  $$\alpha = 2WT_s-1$$

  $$0 \le \alpha \le 1$$

• 带宽与效率：
  • 实际带宽 $W = \frac{1+\alpha}{2T_s}$
  • 带宽效率 $\eta=\frac{R_b}W=\frac{R_s\log_2 M}{(1+\alpha)/(2T_s)}=\frac{2\log_2M}{\alpha+1}$

---

# 基带解调与最优接收

# 解调过程

• 输入：基带信号 $s(t)$ 加上加性高斯白噪声（AWGN） $n(t)$。
• 输出：恢复的符号序列。
• 步骤：
  1. 接收：接收受噪声污染的信号。
  2. 决策：根据接收到的信号，做出最可能的符号判决。
• 性能指标：
  • 信噪比（SNR）：衡量信号质量。
  • 误码率（BER）：衡量解调性能。

# 加性高斯白噪声（AWGN）

• 自相关函数：$R_n(\tau)=\frac{n_0}2\delta(\tau)$。
• 功率谱密度：$S_n(f)=\frac{n_0}2$（功率谱密度在所有频率上均为常数）。
• 高斯过程：高斯过程通过线性时不变（LTI）系统后，输出仍然是高斯过程。

# 信道容量

• AWGN 信道容量：根据香农定理，AWGN 信道的容量 $C$ 为：

  $$C=W\log_2(1+\frac S{n_0W})$$

  其中，$W$ 为信道带宽，$S$ 为平均信号功率，$n_0/2$ 为噪声功率谱密度。

---

# 匹配滤波器（Matched Filter）

匹配滤波器的目标是在采样时刻最大化信噪比。

• 接收器：接收信号 $s_i(t)+n(t)$ 通过匹配滤波器 $h(t)$，输出为 $y(t)=s_0(t)+n_0(t)$。
• SNR 最大化：匹配滤波器能最大化输出信号在采样时刻的信噪比。
• 时域表达式：匹配滤波器的冲激响应 $h(t)$ 是输入脉冲波形 $g(t)$ 的时间反转和共轭。

  $$h(t)=g^*(T_s-t)$$

• 频域表达式：

  $$H(f)=G^*(f)e^{-j2\pi fT_s}$$

• 最大信噪比：

  $$SNR_{max}=\frac{2E_g}{n_0}=\frac{2\int|g(t)|^2dt}{n_0}$$

  其中，$E_g$ 是脉冲波形 $g(t)$ 的能量。
• 局限性：单独使用匹配滤波器时，其输出波形 $g_0(t)$ 可能不满足奈奎斯特准则，从而导致 ISI。

---

# 升余弦平方根滤波器（Squared Root Raised Cosine Filter）

为了同时满足消除 ISI 和最大化 SNR 这两个目标，可以将发送端和接收端滤波器联合设计。

• 思路：将整个发送-信道-接收链路的总体冲激响应设计为升余弦滤波器。
• 实现：
  1. 发送滤波器：其频响为升余弦滤波器频响的平方根。

  $$G(f)=\sqrt{G_{rc}(f)}e^{-j\pi fT_s}$$

  2. 接收（匹配）滤波器：作为发送滤波器的匹配滤波器。

  $$H(f)=G_{m.f.}(f)=G^*(f)e^{-j2\pi fT_s}$$

• 联合效果：两个滤波器串联后的总频响为 $G_0(f)=G(f)H(f)=G_{rc}(f)$，从而在消除 ISI 的同时达到 SNR 最大化。

---

# 信噪比（SNR）的进一步讨论

# 符号与比特的平均能量

• 符号平均能量：$E_s=E[|a_i|^2]\int|g(t)|^2dt$。
• 比特平均能量：$E_b=\frac{E_s}{\log_2M}$。
• 平均信噪比：$\gamma=SNR_{avg}=\frac{2E_s}{n_0}$。

# 整个基带信号的功率谱密度

• 功率谱密度：$S_A(f)=\frac{\sigma_a}{T_s}|G(f)|^2$。
• 总功率：$S=R(0)=\frac{E_s}{T_s}=E_sR_s$。
• 接收端信噪比：

  $$\gamma_B=SNR=\frac{E_sR_s}{n_0W}=\frac{2E_s}{n_0(1+\alpha)}\le\frac{2E_s}{n_0}$$

---

# 等效离散模型

由于采用升余弦平方根滤波器后，系统在采样点上没有 ISI，可以将复杂的连续系统简化为等效的离散模型，便于分析。

• 等效线性关系：

  $$y_i=\bar ga_i+n_i$$

  • $y_i$：第 $i$ 个符号的接收样本。
  • $a_i$：第 $i$ 个符号的发送值。
  • $n_i$：等效噪声。
  • $\bar g$：增益因子，$\bar g=\sqrt{\int |G(f)|^2df}$。
  • 噪声功率：$\sigma^2 = E[n_i^2] = \frac{n_0}{2}$。
• 归一化等效模型：

  $$y_i^\prime=a_i+n_i^\prime$$

  • 归一化噪声功率：$\sigma^{\prime2}=\frac{n_0}{2\int{|G(f)|^2df}}$。