# 基本概念

# 组成部分与系统函数

正向通路系统函数： $H(s)$ ，描述从输入到输出的信号传输。
反馈通路系统函数： $G(s)$ ，描述从输出到反馈点的信号传输。
闭环系统函数： $Q(s)$ ，描述整个反馈系统的输入-输出关系。
$Q(s)=\frac{H(s)}{1+H(s)G(s)}$

# 反馈的主要作用

# 降低系统灵敏度

反馈可以降低系统对正向通路增益变化的灵敏度。

$S^Q_H=\frac{\Delta Q/Q}{\Delta H/H}=\frac{1}{1+GH}$

当反馈量 $GH$ 远大于 1 时，灵敏度会显著降低。

# 逆系统设计

利用反馈原理，可以设计出近似等于其逆系统的系统，用于补偿。

$Q(s)=\frac{K}{1+KP(s)}\approx\frac{1}{P(s)}$

当 $K$ 足够大时，闭环系统的特性将近似于正向通路系统 $P(s)$ 的逆。

# 使不稳定系统稳定

通过反馈，可以将系统极点从右半平面（不稳定）移动到左半平面（稳定），从而稳定系统。

# 目标跟踪（锁相环，PLL）

锁相环是一种典型的反馈系统，用于使一个信号的相位与另一个信号的相位保持同步。

组成部分
- 鉴相器（Phase Detector, PD）：比较输入信号与参考信号的相位差，并输出一个与相位差成比例的电压信号。
- 环路滤波器（Loop Filter, LF）：对鉴相器输出的电压信号进行滤波，去除高频噪声，得到平滑的控制电压。
- 压控振荡器（Voltage-Controlled Oscillator, VCO）：根据滤波后的控制电压产生一个输出信号，该信号的频率和相位与输入信号同步。
工作原理
- 鉴相器检测输入信号和反馈信号之间的相位差，产生误差信号。
- 误差信号通过环路滤波器，控制压控振荡器的输出频率和相位。
- VCO 输出的信号反馈到鉴相器，与输入信号进行比较，直到两者相位同步。
线性化的锁相环 S 域模型
- 闭环系统函数：
  $H_o(s)=\frac{K_dK_oF(s)}{s+K_dK_oF(s)}$
- 误差传递函数：
  $H_e(s)=\frac{s}{s+K_dK_oF(s)}$
环路阶数与跟踪性能
- 一阶环： $F(s)=K_f$ $F (s) = K_{f}$ 。
  - 误差传递函数： $H_e(s)=\frac{s}{s+K_oK_dK_f}$ 。
  - 当输入仅存在初始相位差 $\theta_i(t)=\Delta\theta u(t)$ 时，一阶环可使稳态相位误差收敛为0。
- 二阶环： $F(s)=\frac{\tau_2s+1}{\tau_1s}$ $F (s) = \frac{τ _{2} s + 1}{τ _{1} s}$ 。
  - 特征参数：
    - 自然频率： $\omega_n=\sqrt{\frac{K_dK_o}{\tau_1}}$
    - 阻尼比： $\zeta=\frac{\tau_2\omega_n}{2}$
  - 误差传递函数： $H_e(s)=\frac{s^2}{s^2+2\zeta\omega_n s+\omega_n^2}$ 。
  - 当输入存在初始恒定频率差 $\theta_i(t)=\omega_\Delta t u(t)$ 时，二阶环可使稳态相位误差收敛为0。
- 更高阶环：当输入信号的频率随时间变化（例如，频率斜变 $\theta_i(t)=2\pi f^\prime t^2u(t)$ ）时，需要更高阶的环路才能实现稳态误差为0的跟踪。

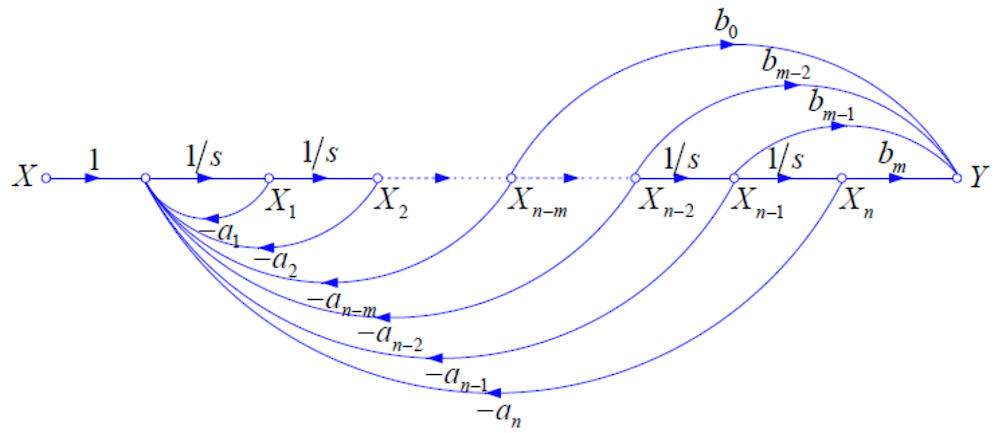
# 信号流图

# 术语定义

结点（Node）：表示系统中变量或信号的点。所有输入到结点的信号叠加，并传递到所有输出支路。
支路（Branch）：连接两个结点的定向线段。支路上的增益称为转移函数。
输入结点/源点（Input Node/Source）：只有输出支路的结点，代表系统的自变量（输入信号）。
输出结点/阱点（Output Node/Sink）：只有输入支路的结点，代表系统的因变量（输出信号）。
混合结点（Mixed Node）：既有输入支路又有输出支路的结点。可通过增加一个单位传输的支路，将其转换为输出结点。
通路（Path）：沿支路箭头方向通过各相连支路的途径。不允许有相反方向的支路。
开通路（Open Path）：通路与任一结点相交不多于一次。
闭通路/环路（Closed Path/Loop）：起点和终点相同的通路，且与任何其他结点相交不多于一次。
环路增益（Loop Gain）：环路中各支路转移函数的乘积。
不接触环路（Non-touching Loops）：两个环路之间没有任何公共结点。
前向通路（Forward Path）：从输入结点到输出结点的通路，且通过任何结点不多于一次。
前向通路增益（Forward Path Gain）：前向通路中各支路转移函数的乘积。
转置（Transposition）：将流图中所有支路的传输方向调转，同时交换输入结点和输出结点，其转移函数保持不变。

# 流图的化简方法

# 图形化简

并联相加，串联相乘：遵循常规电路规则。
混合结点：将混合结点上的输入信号，通过该结点自身的增益，分别传递到所有输出支路，实现解耦。
消除环路：对于有自环的结点，将其所有输入支路增益乘以 $\frac{1}{1-环路增益}$ 来消除自环（由于流图均是加法，反馈公式分母为 $1-环路增益$ ）。

# 代数化简（梅森增益公式）

梅森增益公式（Mason's Gain Formula）用于计算从源点到阱点的总增益。

$H=\frac{1}{\Delta}\sum_k g_k\Delta_k$

$\Delta$ ：流图的特征行列式。
$\begin{align*} \Delta &= 1 - \sum \text{(所有不同环路增益之和)} \\ &\ \ \ \ \ \ \ \ + \sum \text{(每两个互不接触环路增益的乘积之和)} \\ &\ \ \ \ \ \ \ \ - \sum \text{(每三个互不接触环路增益的乘积之和)} + \dots \\ &= 1-\sum_aL_a+\sum_{b,c}L_bL_c-\sum_{d,e,f}L_dL_eL_f+\dots \end{align*}$
$k$ ：表示从源点到阱点的第 $k$ 条前向通路。
$g_k$ ：表示第 $k$ 条前向通路的增益。
$\Delta_k$ ：对于第 $k$ 条前向通路，是除去与该通路相接触的环路后，剩下部分的特征行列式。

# 利用梅森公式画出流图

原理
- 简化流图结构：如果流图中所有环路都互相接触，则 $\Delta=1-\sum\text{(所有不同环路的增益)}$ 。
- 简化通路增益：如果流图中每一条前向通路都与所有环路接触，则 $\Delta_k=1$ 。
- 连续系统实现：连续系统通常用积分器 $1/s$ 来实现。
系统函数对应流图示例
- 考虑一个通用系统函数：
$H(s)=\frac{b_0s^m+b_1s^{m-1}+...+b_m}{s^n+a_1s^{n-1}+...+a_n}=\frac{b_0\frac{1}{s^{n-m}}+b_1\frac{1}{s^{n-m+1}}+...+b_m\frac{1}{s^n}}{1+a_1\frac{1}{s}+...+a_n\frac{1}{s^n}}$
- 该系统函数可以表示为一个信号流图，其中包含串联的积分器和反馈环路，如图所示：