# 概述
小信号放大是电路分析中的重要方法,它通过将非线性电路在某个直流工作点附近进行线性化,从而简化对交流信号的分析。
# 交直流功率分析
总功率Ptotal由直流功率PDC和交流功率PAC两部分组成。其中,交流功率通常使用交流电阻和有效值电压来计算。
Ptotal=PDC+PAC
# 小信号分析步骤
小信号分析通常遵循以下步骤:
- 直流分析:将交流激励置零,进行直流分析,确定非线性元件的工作点。
- 交流分析:将直流激励置零,用微分线性元件替代非线性元件,然后使用线性电路分析方法进行交流分析。
- 元件特性处理:
- 耦合电容:在高频下近似为短路,直流下视为开路。
- 高频扼流圈:在高频下近似为开路,直流下视为短路。
# 常用元件的小信号模型
# 常见非线性元件的微分线性模型
下表列出了常见非线性元件在特定工作区的微分线性模型参数(注意是否考虑厄利效应):
| 非线性元件 |
微分线性模型参数 |
| 二极管(导通区) |
gd=ID0/vT |
| MOSFET(恒流区) |
gm=2ID/Vodgds=ID0/VA |
| BJT(恒流区) |
gm=IC/vTgbe=vTIC0/βgce=IC0/VA |
# 模型应用结论
-
电压放大倍数:将BJT或MOSFET抽象为理想压控流源(如共射/共源组态),若输入等效为戴维南源,输出等效为负载电阻RL′,则电压放大倍数为:
AV=−gmRL′
-
二极管:在小信号分析中通常无需使用交流模型。其原因是微分电阻1/gd在正常使用范围内通常很小(101量级),在交流分析中可近似为短路,因此通常可将二极管视为一个0.7V的恒压源。但在高频下,二极管等效为电容,无法实现原有功能。
-
BJT、MOSFET三种组态的微分线性模型:需要注意的是,除了共射(CE)和共源(CS)组态外,其他两种组态(共基/共栅、共集/共漏)的输入信号不一定是小信号,因为恒流区的线性变化范围较广。
# 晶体管放大器分析
# 三种基本组态
BJT和MOSFET各有三种基本组态:共射(CE)、共基(CB)、共集(CC)和共源(CS)、共栅(CG)、共漏(CD)。
- 组态判定:组态通常根据固定电压端为公共端来判定,或根据信号流动方向来判定。
# 理想情况下的增益
在理想情况下,三种组态的电压增益如下:
- 共射/共源(CE/CS):Ace=Acs=−gmRL′
- 共基/共栅(CB/CG):Acb=Acg=1+gmRS′gmRL′
- 共集/共漏(CC/CD):Ace=Acs=1+gmRL′gmRL′
# 常用看入端口阻抗
以下是几种常用电路结构下的看入端口阻抗计算。
-
图1:
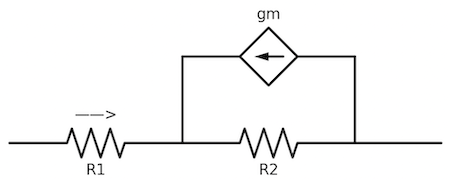
R=R1+R2+gmR1R2
-
图2:
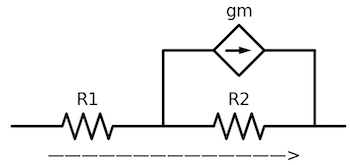
R=1+gmR2R1+R2
-
图3:
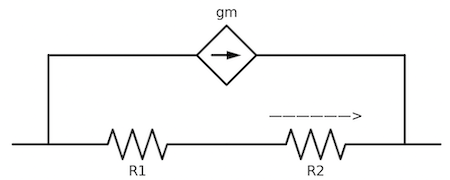
R=1+gmR2R1+R2
# 理想晶体管模型
在一些近似条件下,晶体管可被视为单向网络。
-
共射/共源(CE/CS):
- 近似条件:RS≪rbe,RL≪rce
- 模型:理想跨导模型,可视为理想压控流源。
- 加入负反馈电阻后:仍可视为理想压控压源,跨导增益(非本征)为gmf=1+gmREgm。
-
共基/共栅(CB/CG):
- 近似条件:RL≪rce
- 模型:电流缓冲模型,可视为接近理想的流控流源。
- 特性:输入阻抗Rin=1/gm(较小,等于发射极对地阻抗),输出阻抗Rout=∞,电流增益Ai=−1。
- 与戴维南源级联:此时戴维南源内阻可视为晶体管内部的负反馈电阻,本征跨导增益为gmf=1+gmRSgm。
-
共集/共漏(CC/CD):
- 近似条件:RS≪rbe
- 模型:电压缓冲模型,可视为接近理想的压控压源。
- 特性:输入阻抗Rin=∞,输出阻抗Rout=1/gm(较小,等于发射极对地阻抗),电压增益Av=1。
- 与负载电阻级联:此时负载电阻可视为晶体管内部的负反馈电阻,本征跨导增益为gmf=1+gmRLgm。
# 增益与功率匹配
# 增益类型
增益通常有两种:
- 电压增益
- 功率增益:Gp=VS,rms2/4RSVL,rms2/RL
# 端口匹配与最大功率增益
-
二端口网络匹配条件:为了实现最大功率传输,二端口网络需要满足匹配条件:
ZS=Zin∗ZL=Zout∗
当两个端口同时匹配时,具有最大功率增益。
-
特征阻抗:对于N端口网络,当其余N-1个端口均连接各自的特征阻抗时,该端口的看入阻抗即为其特征阻抗。如果特征阻抗是实数,它就是最大功率传输的匹配阻抗。
-
阻性网络:对于阻性网络,匹配负载为另一个端口在开路和短路时输入电阻的几何平均:
RSm=Rin,2oRin,2sRLm=Rout,1oRout,1s
-
BJT在各种组态下的最大功率增益:对于具有正实数特征阻抗的线性二端口网络,可使用ABCD参数来表示其特征阻抗和最大功率增益。对于BJT,三种组态的最大功率增益近似为:
- 共射(CE):Gp,max=41gm2rberce=41βAv0
- 共基(CB):Gp,max≈gmrce=Av0
- 共集(CC):Gp,max≈gmrbe=Ai0=β


