首页课程笔记统计系应用时间序列分析

# 模型构建

# Box-Jenkins 方法

Box-Jenkins 方法是构建 ARIMA 模型的经典流程，其基本步骤包括：

  1. 确定模型（Identification）： 通过分析时间序列的性质，初步确定模型的类型和阶数。
  2. 估计参数（Estimation）： 利用样本数据估计模型的具体参数。
  3. 模型诊断（Diagnostic Checking）： 检验模型是否恰当，若不通过则返回第一步重新构建。

# ARIMA 模型构建步骤

以下是使用 Box-Jenkins 方法构建 ARIMA 模型的详细步骤：

  1. 数据预处理与平稳性检验

    • 首先绘制时间序列图，直观了解数据的趋势和季节性。
    • 对非平稳时间序列进行变换，如对数变换或差分，直到数据平稳。
    • 计算并分析样本自相关函数（ACF）和偏自相关函数（PACF），确定差分次数 dd。如果时间序列存在单位根，需要持续差分直到其平稳。

  2. 模型定阶

    • 通过分析 ACF、PACF 或 EACF（拓展自相关函数）等相关性图来初步确定模型的阶数 pp 和 qq。
    • 也可以利用信息准则，如 AIC、BIC 或 HQ 等，来选择最优的模型阶数。
    • 相关性方法定阶
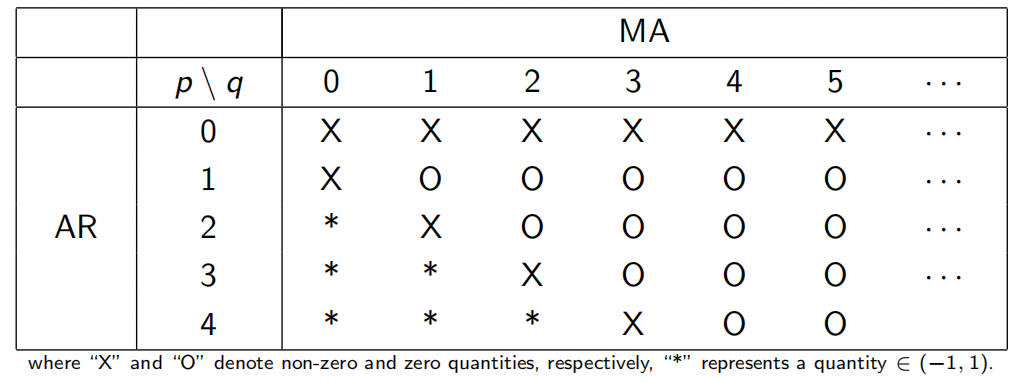
      • MA(q) 模型： ACF 图在滞后 qq 处截断（即 ρj=0,j>q\rho_j = 0, j > q）。
      • AR(p) 模型： PACF 图在滞后 pp 处截断（即 ϕkk=0,k>p\phi_{kk} = 0, k > p）。
      • ARMA(p,q) 模型： 采用 EACF 图，选择左上角且在其右下方向形成三角形的“圈”所对应的位置，该顶点即为 (p,q)(p, q)。
        • 示例图：

  3. 参数估计

    • 用数据估计已确定的 ARIMA(p,d,q)ARIMA(p,d,q) 模型的参数。常用的估计方法包括：
      • AR 模型： 最小二乘估计（LSE）、无条件 LSE、Yule-Walker 估计、条件最大似然估计（MLE）、MLE。
      • ARMA 模型 / MA 模型： 条件 LSE、无条件 LSE、条件 MLE、MLE、最小绝对偏差估计（LADE）。

  4. 模型诊断

    • 对拟合好的模型进行诊断，以确认其能恰当地描述数据。如果诊断不通过，需要重新回到模型定阶步骤。
    • 常用的诊断方法包括：
      • 残差自相关性检验
        • 检验残差的样本 ACF rk(ε^)r_k(\hat{\varepsilon}) 是否接近于0。在原假设（残差无自相关）下，rk(ε^)r_k(\hat{\varepsilon}) 近似服从 N(0,1/n)N(0, 1/n) 分布。
        • Ljung-Box（LB）检验：检验前 mm 个残差 ACF 的联合显著性。

          LB(m)=n(n+2)∑k=1m[rk(ε^)]2n−kLB(m)=n(n+2)\sum_{k=1}^m\frac{[r_k(\hat{\varepsilon})]^2}{n-k}

          在原假设下，LB 统计量近似服从 χm−p−q2\chi^2_{m-p-q} 分布。
        • 拉格朗日乘子（LM）原则。
      • 残差同方差性检验
        • 可通过异方差一致性 tt 统计量进行检验。
        • McLeod-Li（McL）检验：用于检验残差平方的自相关性。

          McL(m)=n(n+2)∑k=1m[rk(ε^2)]2n−kMcL(m)=n(n+2)\sum_{k=1}^m\frac{[r_k(\hat{\varepsilon}^2)]^2}{n-k}

          在原假设下，McL 统计量近似服从 χm−p−q2\chi^2_{m-p-q} 分布。
      • 残差正态性检验
        • 计算残差的偏度 SK^ε^\widehat{SK}_{\hat{\varepsilon}} 和峰度 K^ε^\widehat{K}_{\hat{\varepsilon}}。

          m^j=1n∑t=1nε^tjSK^ε^=m^3m^23, K^ε^=m^4m22^\hat{m}_j=\frac{1}{n}\sum_{t=1}^n\hat{\varepsilon}_t^j \\ \widehat{SK}_{\hat{\varepsilon}}=\frac{\hat{m}_3}{\sqrt{\hat{m}_2^3}},~\widehat{K}_{\hat{\varepsilon}}=\frac{\hat{m}_4}{\hat{m_2^2}}

          在正态性原假设下，n/6⋅SK^ε^∼N(0,1)\sqrt{n/6}\cdot\widehat{SK}_{\hat{\varepsilon}}\sim N(0,1)，n/24⋅(K^ε^−3)∼N(0,1)\sqrt{n/24}\cdot(\widehat{K}_{\hat{\varepsilon}}-3)\sim N(0,1)。
        • Jarque-Bera（JB）检验：对正态性的联合检验。

          JB=n6SK^ε^2+n24(K^ε^−3)2JB=\frac{n}{6}\widehat{SK}_{\hat{\varepsilon}}^2+\frac{n}{24}(\widehat{K}_{\hat{\varepsilon}}-3)^2

          在原假设下，JB 统计量近似服从 χ22\chi^2_2 分布。

# 模型选择信息准则

信息准则旨在平衡模型的拟合优度和复杂性，选择最优的模型。通用形式为：

MSC(p,q)=ln⁡(σ~2(p,q))+cn⋅ψ(p,q)MSC(p,q)=\ln(\tilde{\sigma}^2(p,q))+c_n\cdot\psi(p,q)

  • 赤池信息准则（AIC）

    AIC(p,q)=ln⁡(σ~2(p,q))+2n(p+q)AIC(p,q)=\ln(\tilde{\sigma}^2(p,q))+\frac{2}{n}(p+q)

  • 贝叶斯信息准则（BIC）

    BIC(p,q)=ln⁡(σ~2(p,q))+ln⁡nn(p+q)BIC(p,q)=\ln(\tilde{\sigma}^2(p,q))+\frac{\ln{n}}{n}(p+q)