8. MCMC方法

# Metropolis-Hastings (MH) 算法

# 算法流程

1. 定义目标分布与提议分布

   • 目标分布为 $p(\theta \mid y)$，这是我们希望采样的分布。
   • 提议分布（Proposal Distribution）为 $g(\theta^* \mid \theta^{(t)})$，用于生成新的候选样本 $\theta^*$。

2. 迭代采样过程

   • 给定当前样本 $\theta^{(t)}$。
   • 从提议分布中采样一个候选值：$\theta^* \sim g(\theta \mid \theta^{(t)})$。
   • 计算接受率 $r$：

     $$r = r(\theta^{(t)}, \theta^*) = \frac{p(\theta^* \mid y) / g(\theta^* \mid \theta^{(t)})}{p(\theta^{(t)} \mid y) / g(\theta^{(t)} \mid \theta^*)} = \frac{p(\theta^* \mid y)}{p(\theta^{(t)} \mid y)} \frac{g(\theta^{(t)} \mid \theta^*)}{g(\theta^* \mid \theta^{(t)})}$$

   • 接受或拒绝：以 $\min(1, r)$ 的概率接受 $\theta^*$。
     • 若接受，则设置 $\theta^{(t+1)} = \theta^*$。
     • 若拒绝，则保留当前样本，设置 $\theta^{(t+1)} = \theta^{(t)}$。
   • 为了避免计算精度问题，通常比较 $\log(r)$ 和 $\log(u)$（其中 $u \sim U(0,1)$）。

# 算法特点与效率

• 如果目标函数 $p$ 未归一化，可以用其未归一化的形式 $q$ 代替，算法不受影响。
• 当 $\theta^* = \theta^{(t)}$ 时，接受率 $r=1$，提议总是被接受。
• 理想的提议分布：理论上，最优的提议分布是目标分布本身 $g(\theta \mid \theta^{(t)}) = p(\theta \mid y)$，此时接受率 $r=1$。然而，这在实践中通常无法实现。
• 选择提议分布的原则：
  • 提议分布 $g$ 必须易于采样。
  • 接受率 $r$ 必须易于计算。
  • 采样点 $\theta^{(t)}$ 之间的跳跃（leap）应足够远，以确保马尔可夫链能在整个参数空间中自由探索，但又不能太远（否则接受率过低）。

# 独立提议 Metropolis-Hastings

1. 算法流程

   • 提议分布与当前值独立：$g(\theta \mid \theta^{(t)}) = g(\theta)$。
   • 接受率 $r$ 简化为：

     $$r = \frac{q(\theta^* \mid y) / g(\theta^*)}{q(\theta^{(t)} \mid y) / g(\theta^{(t)})} = \frac{q(\theta^* \mid y)}{q(\theta^{(t)} \mid y)} \frac{g(\theta^{(t)})}{g(\theta^*)}$$

2. 重尾效应

   • 为了确保算法高效，提议分布 $g$ 的尾部应该与目标分布 $p$ 相同或更重。
   • 原因：如果 $p$ 的尾部比 $g$ 更重，当马尔可夫链到达 $p$ 的尾部区域（即 $p(\theta^{(t)} \mid y) \gg g(\theta^{(t)})$）时，任何新提出的非尾部区域的样本 $\theta^*$ 都将以极低的概率被接受，因为：

     $$r = \frac{g(\theta^{(t)})}{p(\theta^{(t)} \mid y)} \frac{p(\theta^* \mid y)}{g(\theta^*)} \approx 0$$

   • 在散点图中，这种效应表现为尾部出现水平带状，这表明马尔可夫链被困在尾部区域，无法有效探索空间。

   

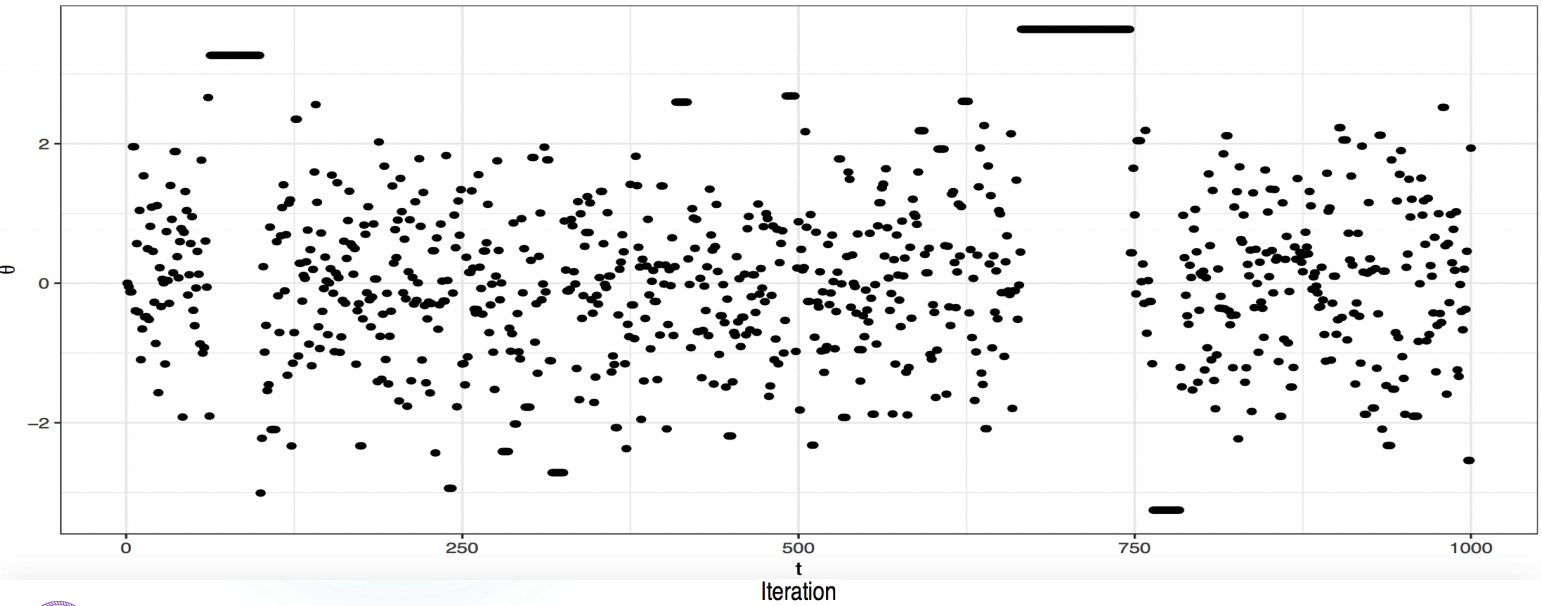
# 随机游走 Metropolis-Hastings

1. 算法流程

   • 提议分布 $g$ 是对称的：$g(\theta^* \mid \theta^{(t)}) = g(\theta^{(t)} \mid \theta^*)$。
   • 接受率 $r$ 简化为：

     $$r = \frac{q(\theta^* \mid y)}{q(\theta^{(t)} \mid y)}$$

   • 一个常见的例子是使用正态分布作为提议分布：$\theta^* \mid \theta^{(t)} \sim N(\theta^{(t)}, v^2 I)$。

2. 参数选择

   • 提议方差 $v^2$ 是一个关键参数。
   • 如果 $v^2 \to 0$，则 $\theta^* \approx \theta^{(t)}$，$r \approx 1$，提议总是被接受，但马尔可夫链移动缓慢，无法充分探索参数空间。
   • 如果 $v^2 \to \infty$，则 $q(\theta^* \mid y) \approx 0$，$r \approx 0$，提议总是被拒绝，马尔可夫链停滞不前。
   • 存在一个最优的方差。对于正态目标分布，当维度为 $d$ 时，最优提议方差为 $2.4^2 \text{Var}(\theta \mid y)/d$。这使得单维度时接受率约为 44%，当 $d \to \infty$ 时，接受率降至 23%。

3. 参数自适应调整

   • 由于目标分布的方差 $\text{Var}(\theta \mid y)$ 通常未知，我们可以通过迭代来估计它。
   • 流程：
     1. 设置一个初始的协方差矩阵 $S_0$。
     2. 进行 MCMC 采样，提议方差为 $2.4^2 S_b/d$。
     3. 使用所有已采样的样本，计算新的协方差矩阵 $S_{b+1}$。
     4. 重复此过程 $B$ 轮。
     5. 最后，丢弃预热（burn-in）阶段的所有样本，并使用最终的协方差矩阵 $S_B$ 进行正式采样。

---

# Gibbs 采样器

# 基本概念

Gibbs 采样器是 MH 算法的一个特例，它通过分解目标分布为一系列条件分布来简化采样过程。每个步骤都从一个完全条件分布中采样，并且接受率 $r$ 始终为 1。

# 二元 Gibbs 采样器

• 前提条件：目标分布为 $p(\theta \mid y)$，其中 $\theta = (\theta_1, \theta_2)$，且完全条件分布 $p(\theta_1 \mid \theta_2, y)$ 和 $p(\theta_2 \mid \theta_1, y)$ 都是已知的且易于采样。

• 算法流程：

  1. 给定初始值 $(\theta_1^{(0)}, \theta_2^{(0)})$。
  2. 重复以下迭代过程：
     • 从第一个完全条件分布中采样：$\theta_1^{(t)} \sim p(\theta_1 \mid \theta_2^{(t-1)}, y)$。
     • 从第二个完全条件分布中采样：$\theta_2^{(t)} \sim p(\theta_2 \mid \theta_1^{(t)}, y)$。

• 例子：如果目标分布是二元正态分布 $\theta \sim N_2(0, \Sigma)$，其中 $\Sigma$ 的协方差为 $\rho$，那么其条件分布是：

  • $\theta_1 \mid \theta_2 \sim N(\rho\theta_2, 1-\rho^2)$
  • $\theta_2 \mid \theta_1 \sim N(\rho\theta_1, 1-\rho^2)$

• 收敛速度：收敛速度取决于变量之间的相关性。相关性越大，马尔可夫链的移动越慢，收敛也越慢。在本例中，收敛速度取决于 $\rho^2$。

# 多元 Gibbs 采样器

• 前提条件：目标分布为 $p(\theta \mid y)$，其中 $\theta = (\theta_1, \dots, \theta_K)$，并且每个分量的完全条件分布 $p(\theta_k \mid \theta_{-k}, y)$ 都是已知的且易于采样（其中 $\theta_{-k}$ 表示除 $\theta_k$ 之外的所有变量）。
• 算法流程：
  1. 给定初始值 $(\theta_1^{(0)}, \dots, \theta_K^{(0)})$。
  2. 重复以下迭代过程：
     • 对于 $k=1, \dots, K$，依次采样：

       $$\theta_k^{(t)} \sim p(\theta_k \mid \theta_1^{(t)}, \dots, \theta_{k-1}^{(t)}, \theta_{k+1}^{(t-1)}, \dots, \theta_K^{(t-1)}, y)$$

  • 注意：在每个步骤中，置于条件的变量都应使用其最新的采样值。

# Gibbs 采样器的变体

• 系统扫描 Gibbs 采样器：按固定的顺序（例如 $1, \dots, K$）依次更新每个参数。
• 随机扫描 Gibbs 采样器：在每次迭代中，随机选择一个参数进行更新。
• 成块（组）Gibbs 采样器：将多个参数组合成一个“块”进行更新，而不是逐个更新。
• 折叠 Gibbs 采样器：通过积分方式移除一些变量，只对剩余的变量进行迭代采样，然后再从其条件分布中直接采样被移除的变量。

---

# Metropolis-within-Gibbs (MwG)

# 主要思想

• 当 Gibbs 采样器中的某个完全条件分布 $p(\theta_k \mid \theta_{-k}, y)$ 不易于直接采样时，可以使用一步 MH 算法来代替。

• 实现方式：在 Gibbs 采样器的迭代中，对难以采样的分量 $\theta_k$，将其完全条件分布 $p(\theta_k \mid \theta_{-k}, y)$ 作为目标分布，并使用 MH 算法进行一次迭代采样。

• 例如，在二元正态模型中，如果 $\theta_1$ 可以用 Gibbs 采样，而 $\theta_2$ 的条件分布难以采样，则可以：

  • 使用 Gibbs 采样 $\theta_1^{(t)} \sim p(\theta_1 \mid \theta_2^{(t-1)}, y)$。
  • 使用 MH 算法采样 $\theta_2^{(t)}$，其目标分布为 $p(\theta_2 \mid \theta_1^{(t)}, y)$。

• MH 算法可以是随机游走 MH，独立提议 MH，甚至是拒绝采样等。