7. 贝叶斯计算基础

# 概述：为什么贝叶斯推断需要采样

在贝叶斯推断中，我们面临的主要挑战是计算的复杂性。无论是参数的后验分布 $p(\theta \mid y)$ 还是后验预测分布 $p(\tilde{y} \mid y)$ ，它们通常都没有封闭形式的解析解，这使得直接进行精确计算变得极其困难。此外，后验分布 $p(\theta \mid y) \propto p(\theta)p(y \mid \theta)$ 往往是非归一化的，进一步加大了计算难度。

蒙特卡洛方法为解决这些问题提供了有效的途径。它的核心思想是通过模拟随机变量函数的样本均值来近似期望值，这种近似是无偏的。利用从后验分布中抽取的样本，我们可以通过数值方法对任何后验统计量进行推断。

# 采样的重要性

采样允许我们通过数值积分来近似期望值。对于一个函数 $h(\theta)$ ，其在后验分布 $p(\theta \mid y)$ 下的期望可以近似表示为：

$E[h(\theta) \mid y] = \int h(\theta)p(\theta \mid y)d\theta \approx \frac{1}{S}\sum_{s=1}^S h(\theta^s)$

其中， $\theta^s$ 是从分布 $p(\theta \mid y)$ 中抽取的样本。根据中心极限定理（CLT），这个近似值的收敛速度为 $O(S^{-1/2})$ 。

许多重要的统计量都可以用期望的形式来表达，例如：

概率： $P(Y \in A) = E[I_{\{A\}}(Y)]$
积分： $\int_a^b q(x)dx = (b-a)\int_a^b q(x)\frac{1}{b-a}dx = (b-a)E[q(U)]$ ，其中 $U$ 是在 $[a, b]$ 上的均匀分布。
求和： $\sum_{x \in A} q(x) = \frac{1}{p}\sum_{x \in A} q(x)p = \frac{1}{p}E[q(W)]$ ，其中 $p = 1/|A|$ ， $W$ 是定义在 $A$ 上的离散均匀分布。

在实际操作中，我们通常需要生成伪随机数。**线性同余生成器（LCG）**是一种简单且常用的方法，其公式为 $X_{n+1} = (aX_n+c) \pmod m$ 。

# 基本采样方法

# 网格法（Grid Method）

基本思想
网格法通过在目标分布的定义域上创建一组均匀的网格点，将连续分布离散化，然后从这个离散分布中进行采样。

算法流程

假设目标分布为 $p(x)$ 。在定义域上选择一组均匀的网格点 $x_1, \dots, x_n$ 。
计算每个网格点的概率密度 $p_i = p(x_i)$ 。
对概率密度进行归一化，得到离散的概率分布 $\tilde{p}_i = p_i / \sum_{j=1}^n p_j$ 。
计算这个离散分布的累积分布函数（CDF） $\tilde{P}_i = \sum_{j=1}^i \tilde{p}_j$ 。
从均匀分布 $U(0,1)$ 中抽取一个样本 $u$ 。
找到满足 $\tilde{P}_{i-1} < u \le \tilde{P}_i$ 的 $x_i$ 作为最终样本。

优缺点

优点：快速简便，适用于任何密度函数，并可轻松扩展到多变量。
缺点：采样结果是基于对真实分布的近似，而非真实分布本身。网格点数目 $n$ 的选择至关重要，过小的 $n$ 会导致较差的近似效果。此方法无法生成所有可能的随机变量值。

# 逆CDF法（Inverse CDF Method）

基本思想
该方法利用了概率积分变换的原理：如果随机变量 $X$ 的 CDF 为 $F(x)$ ，那么 $F(X)$ 服从均匀分布 $U(0,1)$ 。因此，我们可以通过对均匀分布的样本应用逆CDF函数来生成目标分布的样本。

算法流程

找到目标分布的 CDF $F(x)$ 和其逆函数 $F^{-1}(u) = \inf\{x: F(x) > u\}$ 。
从均匀分布 $U(0,1)$ 中抽取一个样本 $u_i$ 。
通过计算 $x_i = F^{-1}(u_i)$ 得到目标分布的样本。

注意事项

有时使用生存函数 $S(x) = 1-F(x)$ 及其逆函数更方便，两者是等价的，因为 $1-U$ 同样服从 $U(0,1)$ 。
对于离散分布，该方法等同于网格法。

优缺点

优点：能够从正确的分布中抽取样本，并且无需像网格法那样担心网格点的问题。
缺点：许多常见分布（如正态分布、Gamma 分布、Beta 分布等）的 CDF 或其逆函数没有封闭形式，难以直接计算。虽然存在近似值，但通常速度较慢，尤其是在分布的尾部。对于包含大量类别的离散分布，确定样本的计算成本可能很高。

# 利用分布之间的关系

基本思想
如果目标分布与某个容易采样的分布存在直接的函数关系，我们可以先从容易采样的分布中抽取样本，然后通过该函数关系进行转换。

示例

正态分布与对数正态分布： $X \sim N(\mu, \sigma^2)$ ，则 $Y = e^X \sim \text{Log}N(\mu, \sigma^2)$ 。
标准正态分布与卡方分布： $X \sim N(0,1)$ ，则 $Y = X^2 \sim \chi_1^2$ 。
Gamma 分布与 Beta 分布： $X_\alpha \sim \text{Gamma}(1, \alpha)$ ， $X_\beta \sim \text{Gamma}(1, \beta)$ ，则 $Y = \frac{X_\alpha}{X_\alpha + X_\beta} \sim \text{Beta}(\alpha, \beta)$ 。
均匀分布与指数分布： $X \sim U(0,1)$ ，则 $Y = -\log X \sim \text{Exp}(1)$ 。

优缺点

优点：能够从正确的分布中抽取样本。
缺点：许多分布之间缺乏有用的关系。此外，像对数、三角函数等计算成本较高，可能导致效率低下。逆CDF法可以被看作是这种方法的一个特例。

# 拒绝采样（Rejection Sampling）

# 核心思想

当目标分布 $f(x)$ 难以直接采样时，我们可以选择从一个易于采样的提议分布 $g(x)$ 中进行采样。这需要找到一个常数 $c > 1$ ，使得 $f(x) \le cg(x)$ 成立。

# 算法流程

从提议分布 $g(x)$ 中抽取一个样本 $x$ 。
从均匀分布 $U(0,1)$ 中抽取一个样本 $u$ 。
如果 $u \le \frac{f(x)}{cg(x)}$ ，则接受 $x$ 作为目标分布的样本。否则，拒绝 $x$ 。
重复以上步骤，直到获得足够数量的样本。

原理
拒绝采样的合理性在于，条件接受的样本 $x$ 正是服从目标分布 $f(x)$ 的。其接受概率为 $P(\text{accept}) = 1/c$ 。为了提高效率，应选择一个能使得常数 $c$ 尽可能小的提议分布 $g(x)$ 。理论上最优的 $c$ 值为 $c = \sup \frac{f(x)}{g(x)}$ 。

# 变种和挑战

未归一化目标分布：即使目标分布 $q(x) = bf(x)$ （其中 $b$ 是未知的归一化常数）未归一化，拒绝采样也同样适用。只需找到 $\tilde{c}$ 使得 $q(x) \le \tilde{c}g(x)$ ，接受率为 $r(x) = \frac{q(x)}{\tilde{c}g(x)}$ 。
高维问题：拒绝采样在高维空间中效率会急剧下降，因为常数 $c$ 通常会变得非常大，导致大多数样本被拒绝。
重尾分布：提议分布 $g(x)$ 必须比目标分布 $f(x)$ 的尾部更“重”，否则无法找到有限的常数 $c$ 满足 $f(x) \le cg(x)$ 。例如，使用正态分布作为提议分布去采样柯西分布是行不通的。

# 自适应拒绝采样（Adaptive Rejection Sampling, ARS）

核心思想
ARS 是一种改进的拒绝采样方法，它在每次拒绝采样后，都会通过新的信息来更新提议分布，使其更接近目标分布，从而提高接受率。

使用前提
该方法要求目标概率密度函数的对数是凹的（log-concave），即其二阶导数小于或等于零。许多常见分布都满足这个条件，如正态分布、均匀分布、Gamma 分布（当 $\alpha \ge 1$ 时）和 Beta 分布（当 $\alpha, \beta \ge 1$ 时）。

算法概述
ARS 的提议分布 $g(x)$ 由一系列在 $\log f(x)$ 函数上的切线所构成的指数分布的组合。由于对数凹函数是单峰的，其提议分布可以是单个或多个指数分布拼接而成。在采样过程中，如果一个样本被拒绝，我们会在该点增加一个新的切线，从而形成一个更紧密的上包络线（即新的提议分布），提高下一次采样的接受概率。

优缺点

优点：能够从正确的分布中抽取样本，并且极其灵活。对于许多对数凹的分布，该方法提供了高效且自动化的采样方式。
缺点：仅限于对数凹分布。并且提议分布的选择和更新过程相对复杂。

# 重要性采样（Importance Sampling）

# 核心思想

重要性采样的核心思想是，如果从目标分布 $f(x)$ 采样困难，我们可以从一个容易采样的提议分布 $g(x)$ 中采样，并通过为每个样本赋予一个权重 $w_x = f(x)/g(x)$ 来纠正由此产生的偏差。

# 算法流程

从提议分布 $g(x)$ 中抽取大量样本 $x_i$ 。
为每个样本计算其权重 $w_i = f(x_i)/g(x_i)$ 。
利用这些带权重的样本 $(x_i, w_i)$ 来近似目标分布下的期望值。

期望值的近似
通过重要性采样，目标分布下函数 $h(X)$ 的期望可以被近似为：

$E_f[h(X)] = \int h(x)f(x)dx = \int h(x)\frac{f(x)}{g(x)}g(x)dx = E_g[h(x)w_x] \approx \frac{1}{n}\sum_{i=1}^n h(x_i)w_i$

如果目标分布 $q(x) = bf(x)$ 未归一化，则期望的近似值为：

$E_f[h(X)] = \frac{E_g[h(x)w_x]}{E_g[w_x]} \approx \frac{\sum_{i=1}^n h(x_i)w_i}{\sum_{i=1}^n w_i} = \sum_{i=1}^n h(x_i)\tilde{w}_i$

其中 $w_i = q(x_i)/g(x_i)$ ， $\tilde{w}_i$ 是归一化的权重。

# 提议分布 $g(x)$ 的选择

一个好的提议分布是重要性采样的关键。它应满足以下条件：

当 $h(x)f(x) \neq 0$ 时， $g(x) > 0$ 。
$g(x)$ 的形状应尽可能接近 $h(x)f(x)$ 的形状。理论上，当 $g(x)$ 与 $h(x)f(x)$ 成正比时，方差最小化为零。
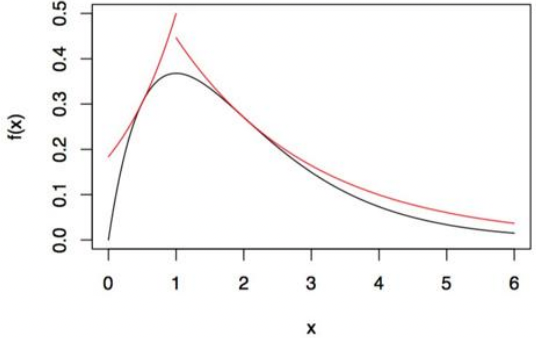
$g(x)$ 应比 $f(x)$ 拥有更重的尾部或相同的尾部，以避免远处的样本权重过大导致的不稳定。
$g(x)$ 必须易于采样，且其概率密度函数易于计算。

在高维空间中，满足这些条件的提议分布往往难以找到。

# 有效样本量（Effective Sample Size, ESS）

有效样本量 $n_{eff}$ 衡量了重要性采样中样本的有效性。它表示与直接从目标分布中抽取 $n_{eff}$ 个样本所获得的方差一致的样本数量。一个常用的近似公式是：

$n_{eff} \approx \frac{n}{1 + CV^2(w)}$

其中 $CV(w)$ 是权重的变异系数。对于归一化的目标分布，更常用的近似是：

$n_{eff} \approx \frac{n}{\frac{1}{n}\sum_{i=1}^n w^2(x_i)}$

对于未归一化的目标分布，有效样本量通常近似为：

$n_{eff} \approx \frac{1}{\sum_{i=1}^n \tilde{w}^2(x_i)}$

其中 $\tilde{w}$ 是归一化后的权重。

# 概述：为什么贝叶斯推断需要采样

# 采样的重要性

# 基本采样方法

# 网格法（Grid Method）

# 逆CDF法（Inverse CDF Method）

# 利用分布之间的关系

# 拒绝采样（Rejection Sampling）

# 核心思想

# 算法流程

# 变种和挑战

# 自适应拒绝采样（Adaptive Rejection Sampling, ARS）

# 重要性采样（Importance Sampling）

# 核心思想

# 算法流程

# 提议分布 g(x)g(x)g(x) 的选择

# 有效样本量（Effective Sample Size, ESS）

6. 贝叶斯模型比较

8. MCMC方法

# 提议分布 $g(x)$ 的选择