首页课程笔记统计系线性回归分析

# 额外平方和（Extra Sum of Squares）

定义与示例

额外平方和（SSR）衡量了在模型中已经包含某些变量的情况下，再加入新的变量后，这些新变量所能解释的额外变异。

  • SSR(X1,X2,X3)SSR(X_1, X_2, X_3)：在模型中，变量 X1,X2,X3X_1, X_2, X_3 联合解释的总变异。
  • SSR(X1∣X2)SSR(X_1|X_2)：在模型中已包含变量 X2X_2 的基础上，加入 X1X_1 后额外解释的变异。
  • SSR(X1,X2∣X3,X4)SSR(X_1, X_2|X_3, X_4)：在模型中已包含 X3,X4X_3, X_4 的基础上，加入 X1,X2X_1, X_2 后额外解释的变异。

计算方式

额外平方和可以通过模型中残差平方和（SSE）或回归平方和（SSR）的差值计算得到。

SSR(X1∣X2)=SSR(X1,X2)−SSR(X2)=SSE(X2)−SSE(X1,X2)SSR(X_1|X_2)=SSR(X_1,X_2)-SSR(X_2)\\=SSE(X_2)-SSE(X_1,X_2)

# 三种平方和（Type I, II, III SS）

平方和的分解

总回归平方和可以分解为一系列额外平方和之和，其分解顺序取决于变量进入模型的顺序。

SSR(X1,X2,X3,X4)=SSR(X1)+SSR(X2∣X1)+SSR(X3∣X1,X2)+SSR(X4∣X1,X2,X3)SSR(X_1,X_2,X_3,X_4)=SSR(X_1)+SSR(X_2|X_1)+SSR(X_3|X_1,X_2)+SSR(X_4|X_1,X_2,X_3)

平方和类型

  • Type I SS：也称序贯平方和，根据变量进入模型的顺序依次计算每个变量所贡献的额外平方和，因此结果与变量的加入顺序相关。
  • Type II SS：考察每个变量在最后进入模型时所贡献的额外平方和，但前提是模型中已有的变量不能包含被考察变量的交互项。例如，SSR(X1∣X1X2)SSR(X_1|X_1X_2) 这种形式是非法的。
  • Type III SS：考察每个变量在最后进入模型时所贡献的额外平方和，与变量的加入顺序无关。在存在交互作用时，这种类型可能违反了边际性原则。
Term Type I SS Type II SS Type III SS
A SSR(A)=SSE(1)−SSE(A)SSR(A) = SSE(\text{1}) - SSE(A) SSR(A∣B)=SSE(B)−SSE(A,B)SSR(A \mid B) = SSE(B) - SSE(A,B) SSR(A∣B,AB)=SSE(B,AB)−SSE(A,B,AB)SSR(A \mid B,AB) = SSE(B,AB) - SSE(A,B,AB)
B SSR(B∣A)=SSE(A)−SSE(A,B)SSR(B \mid A) = SSE(A) - SSE(A,B) SSR(B∣A)=SSE(A)−SSE(A,B)SSR(B \mid A) = SSE(A) - SSE(A,B) SSR(B∣A,AB)=SSE(A,AB)−SSE(A,B,AB)SSR(B \mid A,AB) = SSE(A,AB) - SSE(A,B,AB)
AB SSR(AB∣A,B)=SSE(A,B)−SSE(A,B,AB)SSR(AB \mid A,B) = SSE(A,B) - SSE(A,B,AB) / SSR(AB∣A,B)=SSE(A,B)−SSE(A,B,AB)SSR(AB \mid A,B) = SSE(A,B) - SSE(A,B,AB)

在 R 语言中，ANOVA 函数通常使用 Type I SS，而 Summary 函数则默认使用 Type III SS。

# 广义线性检验（General Linear Test）

基本思想

广义线性检验通过比较两个嵌套模型（一个为全模型 full model，另一个为简化模型 reduction model）来判断它们的差异是否显著。

  • 原假设 H0H_0：两个模型没有显著差异。
  • 备择假设 H1H_1：两个模型有显著差异。
  • 如果拒绝 H0H_0，则表明全模型比简化模型有更强的解释力。

检验统计量

检验统计量 F∗F^* 服从 F 分布。

F∗=(SSE(R)−SSE(F))/(dfE(R)−dfE(F))SSE(F)/dfE(F)=SSR(F∣R)/(dfE(R)−dfE(F))SSE(F)/dfE(F)∼FdfE(R)−dfE(F),dfE(F)F^*=\frac{(SSE(R)-SSE(F))/(df_E(R)-df_E(F))}{SSE(F)/df_E(F)}\\=\frac{SSR(F|R)/(df_E(R)-df_E(F))}{SSE(F)/df_E(F)}\sim F_{df_E(R)-df_E(F),df_E(F)}

  • dfE(R)−dfE(F)df_E(R)-df_E(F)：全模型相比简化模型增加的解释变量数目。
  • dfE(F)=n−pdf_E(F)=n-p：nn 为样本量，pp 为全模型中解释变量的个数加一。
  • 当增加的解释变量数目为 1 时，F1,n−pF_{1,n-p} 等于 tn−p2t^2_{n-p}。

对解释变量线性组合的检验

对于更一般的，对解释变量线性组合的检验，例如 H0:Cβ=tH_0:C\beta=t，检验统计量为：

F=(Cβ^−t)T(C(XTX)−1CT)−1(Cβ^−t)qs2∼Fq,n−pF=\frac{(C\hat \beta-t)^T(C(X^TX)^{-1}C^T)^{-1}(C\hat \beta-t)}{qs^2}\sim F_{q,n-p}

其中 qq 是矩阵 C 独立的行数。

# 偏决定系数（Partial Coefficient of Determination）

多重决定系数 R2R^2 的解读

多重决定系数 R2=SSRSSTR^2=\frac{SSR}{SST} 衡量了所有解释变量所能解释的因变量总变异的比例。

偏决定系数 partial R2partial\ R^2

偏决定系数衡量了在模型中已包含某些解释变量的情况下，新加入的解释变量所能额外解释的，剩余变异（即已有变量不能解释的变异）的比例。

RY;k∣1,...,k−1,k+1,...,q2=SSR(Xk∣X1,...,Xk−1,Xk+1,...,Xq)SSE(X1,...,Xk−1,Xk+1,...,Xq)=SSR(Xk∣X−k)SSE(X−k)R^2_{Y; k|1,...,k-1,k+1,...,q}=\frac{SSR(X_k|X_1,...,X_{k-1},X_{k+1},...,X_q)}{SSE(X_1,...,X_{k-1},X_{k+1},...,X_q)}\\=\frac{SSR(X_k|X_{-k})}{SSE(X_{-k})}

偏决定系数有时也被称为 partial η2partial\ \eta^2。

与决定系数的关系

R2(Y∣X−k,Xk∣X−k)=SSR(Xk∣X−k)SST(Y∣X−k)=SSR(Xk∣X−k)SSE(X−k)=RY;k∣−k2R^2(Y|X_{-k},X_k|X_{-k})=\frac{SSR(X_k|X_{-k})}{SST(Y|X_{-k})}\\=\frac{SSR(X_k|X_{-k})}{SSE(X_{-k})}=R^2_{Y; k|-k}

计算方式

计算 RY;k∣−k2R^2_{Y; k|-k} 的步骤如下：

  1. 首先，用已有的变量 X1,...,Xk−1,Xk+1,...,XqX_1,...,X_{k-1},X_{k+1},...,X_q 分别对因变量 YY 和新变量 XkX_k 进行回归，得到各自的残差，记为 Y∣X−kY|X_{-k} 和 Xk∣X−kX_k|X_{-k}。
  2. 然后，用 Xk∣X−kX_k|X_{-k} 对 Y∣X−kY|X_{-k} 进行回归，得到的决定系数就是偏决定系数。

# 偏相关系数与标准化回归

偏相关系数 r12⋅3r_{12·3}

偏相关系数是偏决定系数开根号后加上符号，用于衡量在排除其他变量影响后，两个变量之间线性关系的强度。

  • 幅度：η2\sqrt{\eta^2}
  • 符号：与对应标准化回归系数的符号一致，sgn(βk)sgn(\beta_k)。
  • 如果 0<r12⋅3<r120<r_{12·3}<r_{12}，说明变量 3 部分解释了变量 1 和 2 之间的线性关系。

标准化回归

通过对所有变量进行标准化（减去均值并除以标准差），可以将回归模型转换为标准化形式，从而使不同变量的回归系数具有可比性。

Yi∗=βi∗Xi1∗+β2∗Xi2∗+...+β(p−1)∗Xi(p−1)∗+εi∗Y^*_i=\beta^*_iX^*_{i1}+\beta^*_2X^*_{i2}+...+\beta^*_{(p-1)}X^*_{i{(p-1)}}+\varepsilon^*_i

其中 βk∗=βksXksY\beta^*_k=\frac{\beta_ks_{Xk}}{s_Y}。

标准化对检验的影响

  • R2,η2R^2, \eta^2 等保持不变。
  • ANOVA 检验结果会改变。
  • 如果只对解释变量 X 进行标准化，而不对因变量 Y 标准化，则 ANOVA 检验结果不变，因为 SST（总平方和）没有变化。

偏相关系数与相关系数的关系

RY⋅2∣12=(rY⋅2∣1)2=(rY2−rY1r12)2(1−rY12)(1−r122)R^2_{Y·2|1}=(r_{Y·2|1})^2=\frac{(r_{Y2}-r_{Y1}r_{12})^2}{(1-r^2_{Y1})(1-r^2_{12})}

当解释变量彼此不相关时，分别用 Y∼X2Y\sim X_2 和 Y∼X1+X2Y\sim X_1+X_2 进行回归，回归系数 b2b_2 保持不变，但 RY⋅2∣12>RY⋅22R^2_{Y·2|1}>R^2_{Y·2}。

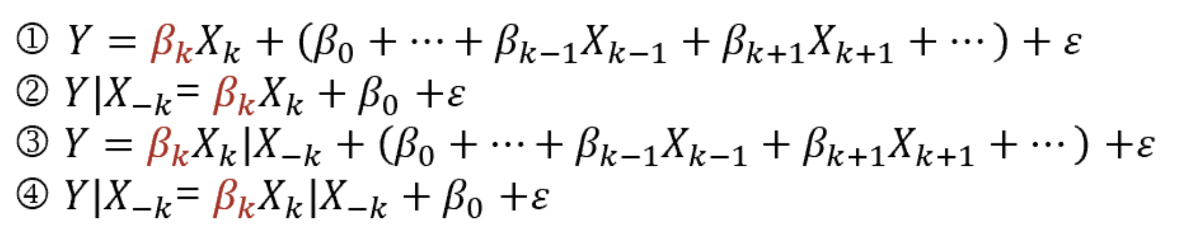
# 抑制变量（Suppressor Variable）

如果一个变量 X1X_1 能够抑制其他自变量的无关变异，导致 SSR(X2∣X1)>SSR(X2)SSR(X_2|X_1)>SSR(X_2)，那么这个变量 X1X_1 就被称为抑制变量。