4. SLR诊断与补救

# 诊断

# 解释变量 ($X$) 的诊断

解释变量的诊断旨在识别潜在的混杂因子，并分析其分布特征。

• 集中趋势与离散程度： 均值、方差、范围。
• 分布形态：
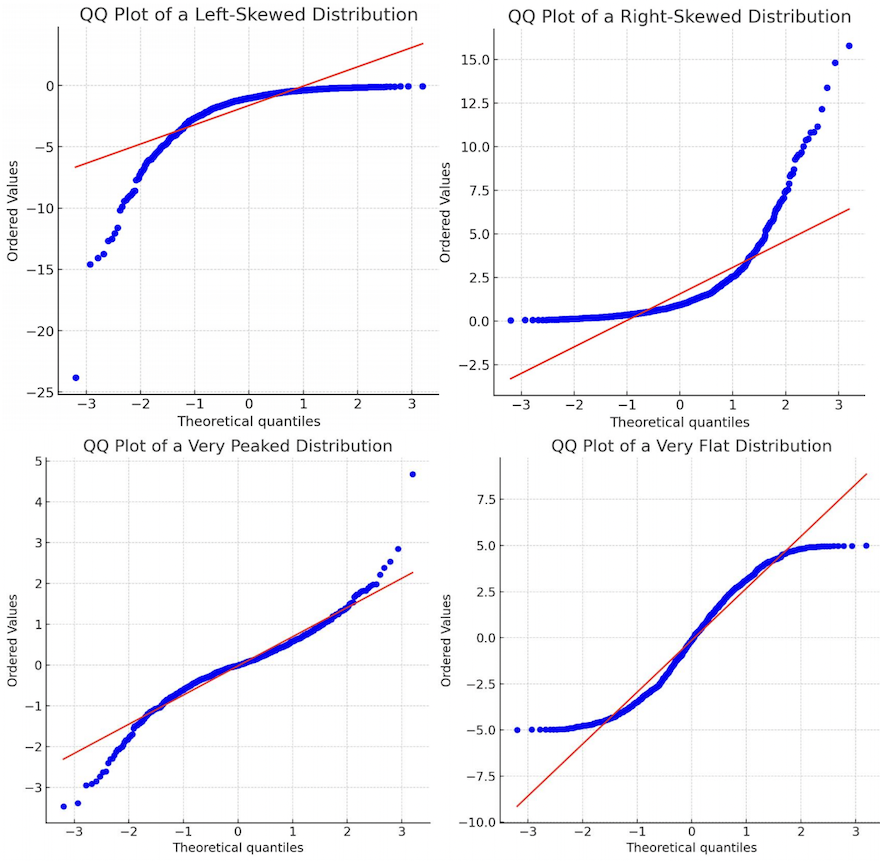
  • 偏度 (Skewness)： 衡量数据分布的对称性。

    $$g_1=\frac{m_3}{m_2^{3/2}}=\frac{\frac1n\sum_i(x_i-\bar x)^3}{(\frac1n\sum_i(x_i-\bar x)^2)^{3/2}}$$

    • $g_1 > 0$：正偏或右偏分布，右侧尾部较长，通常均值 > 中位数 > 众数。
    • $g_1 < 0$：负偏或左偏分布，左侧尾部较长，通常均值 < 中位数 < 众数。
  • 峰度 (Kurtosis)： 衡量数据分布的尖峭程度（尾部厚度）。

    $$g_2=\frac{m_4}{m_2^2}-3=\frac{\frac1n\sum_i(x_i-\bar x)^4}{(\frac1n\sum_i(x_i-\bar x)^2)^{2}}-3$$

    • $g_2 > 0$：尖峰态分布（Leptokurtic），尾部较重。
    • $g_2 < 0$：低峰态分布（Platykurtic），尾部较轻。
• QQ 图 (Quantile-Quantile Plot)： 用于检验数据是否服从某种特定分布（如正态分布）。

# 常用诊断图

• stem： 茎叶图，用于显示数据分布。
• boxplot： 箱线图，用于识别异常值和数据分布情况。
• hist： 柱状图，直观展示数据频率分布。
• qqnorm, qqline： 用于生成和绘制正态 QQ 图，判断数据是否近似正态分布。

# 残差诊断

残差诊断是检验线性回归模型基本假设的关键步骤。

• 线性关系： 通过**残差图（Residuals vs Fitted）**检查，期望残差均匀分布在0值附近。可使用 plot, abline, scatter.smooth 等函数。
• 方差齐性 (Homoscedasticity)： 检查残差方差是否恒定。
  • 图示： 通过**残差图（Residuals vs Fitted）**或 Scale-Location Plot 检查，期望残差的散点均匀分散，没有明显的扇形或漏斗形。
  • 检验方法： * Bartlett's test (对正态性敏感)
    • Levene's test (较常用)
    • Brown-Forsythe test (较常用)
    • Breusch-Pagan test
• 正态性： 检查残差是否服从正态分布。
  • 图示： 通过正态 QQ 图、箱线图、柱状图等。
  • 检验方法： * Shapiro-Wilk test (较常用，shapiro.test)
    • Kolmogorov-Smirnov test
    • Cramér-von Mises test
    • Anderson-Darling test
• 相关性 (独立性)： 检查残差是否相互独立。
  • Durbin-Watson test
  • Ljung-Box test
• 离群值 (Outliers)： 通过残差图识别与模型预测值相差较大的点。

# 异常值、杠杆值与强影响力点

• 异常值（Outlier）： 在 Y 轴上远离回归直线的点，残差值大。
• 杠杆值（Leverage Point）： 在 X 轴上远离数据中心均值的点，对回归系数影响大。$h_{ii}$ 用来衡量杠杆值。
• 强影响力点（Influential Point）： 同时是异常值和杠杆值的点，对回归直线有不成比例的巨大影响。

# 离群值相关指标

• 半学生化残差 (Semistudentized Residual)： $$
  t_i=\frac{e_i}{\sqrt{MSE}}

  $$$$

  $$var(e_i)=\sigma^2(1-h_{ii}) \\ t_i=\frac{e_i}{\sqrt{MSE(1-h_{ii})}}$$

• 剔除学生化残差 (Studentized Deleted Residual)： 移除第 $i$ 个点后，用剩余数据拟合模型，再计算其残差。

  $$d_i=Y_i-\hat Y_{i(-i)} \\ t_i=\frac{d_i}{s(d_i)}=\frac{e_i}{\sqrt{MSE_i(1-h_{ii})}}$$

• 库克距离 (Cook's Distance)： 衡量一个点对所有预测值的影响，常用于识别强影响力点。

  $$D_i=\frac{\sum_j(\hat Y_j-\hat Y_{j(-i)})^2}{ps^2}=\frac{e_i^2}{ps^2}\frac{h_{ii}}{(1-h_{ii})^2}$$

  • $h_{ii}$ 是帽子矩阵 $H$ 的对角元，$\hat Y=HY$，表示杠杆值大小。
  • 残差 vs 杠杆值图 (Residuals vs Leverage)： 结合残差和杠杆值，通过库克距离等高线识别强影响力点，重点关注右上角和右下角的点。

# 拟合诊断图总结

• Residuals vs Fitted： 检查非线性、不等方差、过拟合和异常值。
• Normal Q-Q Plot： 检验残差正态性。
• Scale-Location Plot： 检验方差齐性。
• Residuals vs Leverage： 识别强影响力点。

---

# 补救与其它

# 失拟检验 (Lack of Fit Test)

失拟检验用于判断回归模型是否能够很好地拟合数据，即是否存在非线性关系。

• 原假设 ($H_0$)： 线性回归模型拟合能力足够。
• 广义似然比检验 (GLT)： 比较“完全模型”（Full Model）与“简化模型”（Reduced Model）的拟合效果。
• 方差分析表 (ANOVA)：
  • $SST = SSE + SSR$
  • $SSE = SSPE + SSLF$
  • 失拟平方和 (SSLF)： 衡量模型无法解释的变异。
  • 纯误差平方和 (SSPE)： 衡量数据内在的随机变异。
  • $F$ 统计量： $F = \frac{MSLF}{MSPE} \sim F_{c-2,n-c}$。
• R 语言： lm(Y ~ 0 + as.factor(X), data = data) 用于拟合完全模型。

# 非线性关系的补救

• 非线性变换： 通过对 Y 或 X 进行函数变换，将非线性关系转换为线性关系。
• 稳定方差变换： 如果方差不齐，可以通过变换 $Y$ 来稳定方差。

  $$f(\mu)=\int \frac{cd\mu}{\sqrt{h(\mu)}}$$

• Box-Cox 变换： 一种常用的幂变换，用于同时解决非线性和方差不齐的问题。

  $$Y^*=\frac{Y^\lambda-1}{\lambda}$$

  • 最佳 $\lambda$ 值通过最小化 SSE 获得。
  • 置信区间： $\{\lambda|\log L(\lambda) \ge\log L(\hat\lambda)-\frac12\chi^2_{1,1-\alpha} \}$
  • R 语言： boxcox 函数。

# 过原点的回归拟合

• 模型： lm(Y ~ 0 + X)
• 系数估计： $b=\frac{\sum_iX_iY_i}{\sum_i X_i^2}$
• 特点：
  • $cov(b,\bar Y) \ne 0$
  • $\sum_i e_i \ne 0$
  • $SST \ne SSE + SSR$

# 逆向回归

• 目的： 用 Y 预测 X。
• 模型： $\hat X_h=\frac{Y_h-b_0}{b_1}$
• 与正向回归的关系： * $a_1b_1 = r^2$
  • 两者的回归线通常不重合，除非 $r=\pm1$。

# $R^2$ 与调整 $R^2$ 的局限性

• 无法完全衡量模型契合度： 高 $R^2$ 不一定代表模型拟合良好。
• 无法衡量预测能力： 高 $R^2$ 的模型在预测新数据时可能表现不佳。
• 无法比较经过变换后的模型： 不同变换后的模型 $R^2$ 不具可比性。
• 无法说明因果关系： $R^2$ 只衡量变量间的关联强度，不能解释一个变量对另一个变量的因果作用。